We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

TEXT
Unlock Solution Steps
Sign in to
Symbolab
Get full access to all Solution Steps for any math problem
By continuing, you agree to our Terms of Use
and have read our Privacy Policy

Study Guides > Intermediate Algebra

Read: Graph an Inequality in Two Variables

Learning Objectives

  • Identify and follow steps for graphing a linear inequality in two variables
So how do you get from the algebraic form of an inequality, like [latex]y>3x+1[/latex], to a graph of that inequality? Plotting inequalities is fairly straightforward if you follow a couple steps.

Graphing Inequalities

To graph an inequality:
  • Graph the related boundary line. Replace the <, >, ≤ or ≥ sign in the inequality with = to find the equation of the boundary line.
  • Identify at least one ordered pair on either side of the boundary line and substitute those [latex](x,y)[/latex] values into the inequality. Shade the region that contains the ordered pairs that make the inequality a true statement. 
  • If points on the boundary line are solutions, then use a solid line for drawing the boundary line. This will happen for ≤ or ≥ inequalities.
  • If points on the boundary line aren’t solutions, then use a dotted line for the boundary line. This will happen for < or > inequalities.
Let’s graph the inequality [latex]x+4y\leq4[/latex]. To graph the boundary line, find at least two values that lie on the line [latex]x+4y=4[/latex]. You can use the x- and y-intercepts for this equation by substituting [latex]0[/latex] in for x first and finding the value of y; then substitute [latex]0[/latex] in for y and find x.
x y
[latex]0[/latex] [latex]1[/latex]
[latex]4[/latex] [latex]0[/latex]
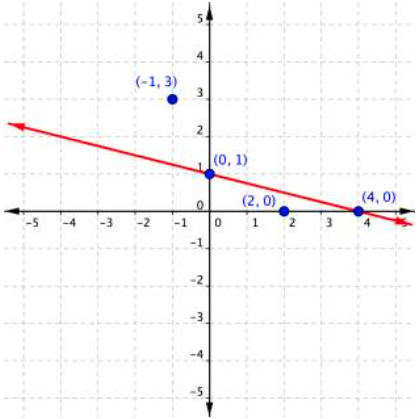Plot the points [latex](0,1)[/latex] and [latex](4,0)[/latex], and draw a line through these two points for the boundary line. The line is solid because ≤ means “less than or equal to,” so all ordered pairs along the line are included in the solution set. Solid downward-sloping line that crosses the points (0,1) and (4,0). The point (-1,3) and the point (2,0) are also plotted. The next step is to find the region that contains the solutions. Is it above or below the boundary line? To identify the region where the inequality holds true, you can test a couple of ordered pairs, one on each side of the boundary line. If you substitute [latex](−1,3)[/latex] into [latex]x+4y\leq4[/latex]:

[latex]\begin{array}{r}−1+4\left(3\right)\leq4\\−1+12\leq4\\11\leq4\end{array}[/latex]

This is a false statement, since [latex]11[/latex] is not less than or equal to [latex]4[/latex]. On the other hand, if you substitute [latex](2,0)[/latex] into [latex]x+4y\leq4[/latex]:

[latex]\begin{array}{r}2+4\left(0\right)\leq4\\2+0\leq4\\2\leq4\end{array}[/latex]

This is true! The region that includes [latex](2,0)[/latex] should be shaded, as this is the region of solutions.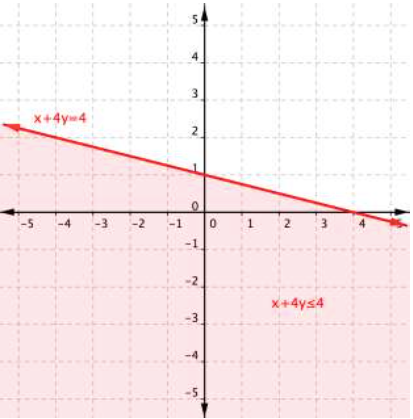 Solid downward-sloping line marked x+4y=4. The region below the line is shaded and is labeled x+4y is less than or equal to 4. And there you have it—the graph of the set of solutions for [latex]x+4y\leq4[/latex].

Graphing Linear Inequalities in Two Variables

https://youtu.be/2VgFg2ztspI

Example

Graph the inequality [latex]2y>4x–6[/latex].

Answer: Solve for y.

[latex] \displaystyle \begin{array}{r}2y>4x-6\\\\\dfrac{2y}{2}>\dfrac{4x}{2}-\dfrac{6}{2}\\\\y>2x-3\\\end{array}[/latex]

Create a table of values to find two points on the line [latex] \displaystyle y=2x-3[/latex], or graph it based on the slope-intercept method, the b value of the y-intercept is [latex]-3[/latex] and the slope is [latex]2[/latex]. Plot the points, and graph the line. The line is dotted because the sign in the inequality is >, not ≥ and therefore points on the line are not solutions to the inequality.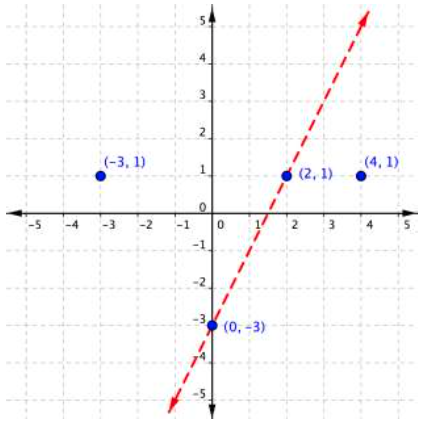 Dotted upward-sloping line that crosses the points (2,1) and (0,-3). The points (-3,1) and (4,1) are also plotted.

[latex] \displaystyle y=2x-3[/latex]

x y
[latex]0[/latex] [latex]−3[/latex]
[latex]2[/latex] [latex]1[/latex]
Find an ordered pair on either side of the boundary line. Insert the x- and y-values into the inequality [latex]2y>4x–6[/latex] and see which ordered pair results in a true statement. Since [latex](−3,1)[/latex] results in a true statement, the region that includes [latex](−3,1)[/latex] should be shaded.

[latex]\begin{array}{l}2y>4x–6\\\\\text{Test }1:\left(−3,1\right)\\2\left(1\right)>4\left(−3\right)–6\\\,\,\,\,\,\,\,2>–12–6\\\,\,\,\,\,\,\,2>−18\\\text{TRUE}\\\\\text{Test }2:\left(4,1\right)\\2(1)>4\left(4\right)– 6\\\,\,\,\,\,\,2>16–6\\\,\,\,\,\,\,2>10\\\text{FALSE}\end{array}[/latex]

Answer

The graph of the inequality [latex]2y>4x–6[/latex] is: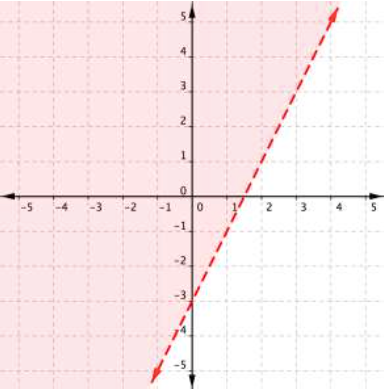 The dotted upward-sloping line of 2y=4x-6, with the region above the line shaded.

A quick note about the problem above—notice that you can use the points [latex](0,−3)[/latex] and [latex](2,1)[/latex] to graph the boundary line, but that these points are not included in the region of solutions, since the region does not include the boundary line!

Graphing Linear Inequalities in Two Variables (Slope Intercept Form)

https://youtu.be/Hzxc4HASygU

Summary

When inequalities are graphed on a coordinate plane, the solutions are located in a region of the coordinate plane, which is represented as a shaded area on the plane. The boundary line for the inequality is drawn as a solid line if the points on the line itself do satisfy the inequality, as in the cases of ≤ and ≥. It is drawn as a dashed line if the points on the line do not satisfy the inequality, as in the cases of < and >. You can tell which region to shade by testing some points in the inequality. Using a coordinate plane is especially helpful for visualizing the region of solutions for inequalities with two variables.

Licenses & Attributions

CC licensed content, Original

  • Ex 1: Graphing Linear Inequalities in Two Variables (Slope Intercept Form). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.

CC licensed content, Shared previously

  • Ex 2: Graphing Linear Inequalities in Two Variables (Standard Form). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.