We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

TEXT
Unlock Solution Steps
Sign in to
Symbolab
Get full access to all Solution Steps for any math problem
By continuing, you agree to our Terms of Use
and have read our Privacy Policy

Study Guides > MATH 0123

Linear Inequalities and Absolute Value Inequalities

Learning Outcomes

  • Use interval notation to express inequalities.
  • Use properties of inequalities.
  • Solve compound inequalities.
  • Solve absolute value inequalities.
It is not easy to make the honor roll at most top universities. Suppose students were required to carry a course load of at least 12 credit hours and maintain a grade point average of 3.5 or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore various ways to express different sets of numbers, inequalities, and absolute value inequalities. Several red winner’s ribbons lie on a white table.

Writing and Manipulating Inequalities

Indicating the solution to an inequality such as [latex]x\ge 4[/latex] can be achieved in several ways. We can use a number line as shown below. The blue ray begins at [latex]x=4[/latex] and, as indicated by the arrowhead, continues to infinity, which illustrates that the solution set includes all real numbers greater than or equal to 4. A number line starting at zero with the last tick mark being labeled 11. There is a dot at the number 4 and an arrow extends toward the right. We can use set-builder notation: [latex]\{x|x\ge 4\}[/latex], which translates to "all real numbers x such that x is greater than or equal to 4." Notice that braces are used to indicate a set. The third method is interval notation, where solution sets are indicated with parentheses or brackets. The solutions to [latex]x\ge 4[/latex] are represented as [latex]\left[4,\infty \right)[/latex]. This is perhaps the most useful method as it applies to concepts studied later in this course and to other higher-level math courses. The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be "equaled." A few examples of an interval, or a set of numbers in which a solution falls, are [latex]\left[-2,6\right)[/latex], or all numbers between [latex]-2[/latex] and [latex]6[/latex], including [latex]-2[/latex], but not including [latex]6[/latex]; [latex]\left(-1,0\right)[/latex], all real numbers between, but not including [latex]-1[/latex] and [latex]0[/latex]; and [latex]\left(-\infty ,1\right][/latex], all real numbers less than and including [latex]1[/latex]. The table below outlines the possibilities.
Set Indicated Set-Builder Notation Interval Notation
All real numbers between a and b, but not including a or b [latex]\{x|a<x<b\}[/latex] [latex]\left(a,b\right)[/latex]
All real numbers greater than a, but not including a [latex]\{x|x>a\}[/latex] [latex]\left(a,\infty \right)[/latex]
All real numbers less than b, but not including b [latex]\{x|x<b\}[/latex] [latex]\left(-\infty ,b\right)[/latex]
All real numbers greater than a, including a [latex]\{x|x\ge a\}[/latex] [latex]\left[a,\infty \right)[/latex]
All real numbers less than b, including b [latex]\{x|x\le b\}[/latex] [latex]\left(-\infty ,b\right][/latex]
All real numbers between a and b, including a [latex]\{x|a\le x<b\}[/latex] [latex]\left[a,b\right)[/latex]
All real numbers between a and b, including b [latex]\{x|a<x\le b\}[/latex] [latex]\left(a,b\right][/latex]
All real numbers between a and b, including a and b [latex]\{x|a\le x\le b\}[/latex] [latex]\left[a,b\right][/latex]
All real numbers less than a or greater than b [latex]\{x|x<a\text{ and }x>b\}[/latex] [latex]\left(-\infty ,a\right)\cup \left(b,\infty \right)[/latex]
All real numbers [latex]\{x|x\text{ is all real numbers}\}[/latex] [latex]\left(-\infty ,\infty \right)[/latex]

Example: Using Interval Notation to Express All Real Numbers Greater Than or Equal to a Number

Use interval notation to indicate all real numbers greater than or equal to [latex]-2[/latex].

Answer: Use a bracket on the left of [latex]-2[/latex] and parentheses after infinity: [latex]\left[-2,\infty \right)[/latex]. The bracket indicates that [latex]-2[/latex] is included in the set with all real numbers greater than [latex]-2[/latex] to infinity.

Try It

Use interval notation to indicate all real numbers between and including [latex]-3[/latex] and [latex]5[/latex].

Answer: [latex-display]\left[-3,5\right][/latex-display]

Example: Using Interval Notation to Express All Real Numbers Less Than or Equal to a or Greater Than or Equal to b

Write the interval expressing all real numbers less than or equal to [latex]-1[/latex] or greater than or equal to [latex]1[/latex].

Answer: We have to write two intervals for this example. The first interval must indicate all real numbers less than or equal to 1. So, this interval begins at [latex]-\infty [/latex] and ends at [latex]-1[/latex], which is written as [latex]\left(-\infty ,-1\right][/latex]. The second interval must show all real numbers greater than or equal to [latex]1[/latex], which is written as [latex]\left[1,\infty \right)[/latex]. However, we want to combine these two sets. We accomplish this by inserting the union symbol, [latex]\cup [/latex], between the two intervals.

[latex]\left(-\infty ,-1\right]\cup \left[1,\infty \right)[/latex]

Try It

Express all real numbers less than [latex]-2[/latex] or greater than or equal to 3 in interval notation.

Answer: [latex-display]\left(-\infty ,-2\right)\cup \left[3,\infty \right)[/latex-display]

Using the Properties of Inequalities

When we work with inequalities, we can usually treat them similarly to but not exactly as we treat equations. We can use the addition property and the multiplication property to help us solve them. The one exception is when we multiply or divide by a negative number, we must reverse the inequality symbol.

A General Note: Properties of Inequalities

[latex]\begin{array}{ll}\text{Addition Property}\hfill& \text{If }a< b,\text{ then }a+c< b+c.\hfill \\ \hfill & \hfill \\ \text{Multiplication Property}\hfill & \text{If }a< b\text{ and }c> 0,\text{ then }ac< bc.\hfill \\ \hfill & \text{If }a< b\text{ and }c< 0,\text{ then }ac> bc.\hfill \end{array}[/latex]

These properties also apply to [latex]a\le b[/latex], [latex]a>b[/latex], and [latex]a\ge b[/latex].

Example: Demonstrating the Addition Property

Illustrate the addition property for inequalities by solving each of the following:
  1. [latex]x - 15<4[/latex]
  2. [latex]6\ge x - 1[/latex]
  3. [latex]x+7>9[/latex]

Answer: The addition property for inequalities states that if an inequality exists, adding or subtracting the same number on both sides does not change the inequality. 1. [latex-display]\begin{array}{ll}x - 15<4\hfill & \hfill \\ x - 15+15<4+15 \hfill & \text{Add 15 to both sides.}\hfill \\ x<19\hfill & \hfill \end{array}[/latex-display] 2. [latex-display]\begin{array}{ll}6\ge x - 1\hfill & \hfill \\ 6+1\ge x - 1+1\hfill & \text{Add 1 to both sides}.\hfill \\ 7\ge x\hfill & \hfill \end{array}[/latex-display] 3. [latex-display]\begin{array}{ll}x+7>9\hfill & \hfill \\ x+7 - 7>9 - 7\hfill & \text{Subtract 7 from both sides}.\hfill \\ x>2\hfill & \hfill \end{array}[/latex-display]

Try It

Solve [latex]3x - 2<1[/latex].

Answer: [latex-display]x<1[/latex-display]

Example: Demonstrating the Multiplication Property

Illustrate the multiplication property for inequalities by solving each of the following:
  1. [latex]3x<6[/latex]
  2. [latex]-2x - 1\ge 5[/latex]
  3. [latex]5-x>10[/latex]

Answer: 1. [latex-display]\begin{array}{l}3x<6\hfill \\ \frac{1}{3}\left(3x\right)<\left(6\right)\frac{1}{3}\hfill \\ x<2\hfill \end{array}[/latex-display] 2. [latex-display]\begin{array}{ll}-2x - 1\ge 5\hfill & \hfill \\ -2x\ge 6\hfill & \hfill \\ \left(-\frac{1}{2}\right)\left(-2x\right)\ge \left(6\right)\left(-\frac{1}{2}\right)\hfill & \text{Multiply by }-\frac{1}{2}.\hfill \\ x\le -3\hfill & \text{Reverse the inequality}.\hfill \end{array}[/latex-display] 3. [latex-display]\begin{array}{ll}5-x>10\hfill & \hfill \\ -x>5\hfill & \hfill \\ \left(-1\right)\left(-x\right)>\left(5\right)\left(-1\right)\hfill & \text{Multiply by }-1.\hfill \\ x<-5\hfill & \text{Reverse the inequality}.\hfill \end{array}[/latex-display]

Try It

Solve [latex]4x+7\ge 2x - 3[/latex].

Answer: [latex]x\ge -5[/latex]

Solving Inequalities in One Variable Algebraically

As the examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations; we combine like terms and perform operations. To solve, we isolate the variable.

Example: Solving an Inequality Algebraically

Solve the inequality: [latex]13 - 7x\ge 10x - 4[/latex].

Answer: Solving this inequality is similar to solving an equation up until the last step.

[latex]\begin{array}{ll}13 - 7x\ge 10x - 4\hfill & \hfill \\ 13 - 17x\ge -4\hfill & \text{Move variable terms to one side of the inequality}.\hfill \\ -17x\ge -17\hfill & \text{Isolate the variable term}.\hfill \\ x\le 1\hfill & \text{Dividing both sides by }-17\text{ reverses the inequality}.\hfill \end{array}[/latex]
The solution set is given by the interval [latex]\left(-\infty ,1\right][/latex], or all real numbers less than and including 1.

Try It

Solve the inequality and write the answer using interval notation: [latex]-x+4<\frac{1}{2}x+1[/latex].

Answer: [latex]\left(2,\infty \right)[/latex]

Example: Solving an Inequality with Fractions

Solve the following inequality and write the answer in interval notation: [latex]-\frac{3}{4}x\ge -\frac{5}{8}+\frac{2}{3}x[/latex].

Answer: We begin solving in the same way we do when solving an equation.

[latex]\begin{array}{ll}-\frac{3}{4}x\ge -\frac{5}{8}+\frac{2}{3}x\hfill & \hfill \\ -\frac{3}{4}x-\frac{2}{3}x\ge -\frac{5}{8}\hfill & \text{Put variable terms on one side}.\hfill \\ -\frac{9}{12}x-\frac{8}{12}x\ge -\frac{5}{8}\hfill & \text{Write fractions with common denominator}.\hfill \\ -\frac{17}{12}x\ge -\frac{5}{8}\hfill & \hfill \\ x\le -\frac{5}{8}\left(-\frac{12}{17}\right)\hfill & \text{Multiplying by a negative number reverses the inequality}.\hfill \\ x\le \frac{15}{34}\hfill & \hfill \end{array}[/latex]
The solution set is the interval [latex]\left(-\infty ,\frac{15}{34}\right][/latex].

Try It

Solve the inequality and write the answer in interval notation: [latex]-\frac{5}{6}x\le \frac{3}{4}+\frac{8}{3}x[/latex].

Answer: [latex-display]\left[-\frac{3}{14},\infty \right)[/latex-display]

Compound and Absolute Value Inequalities

A compound inequality includes two inequalities in one statement. A statement such as [latex]4<x\le 6[/latex] means [latex]4<x[/latex] and [latex]x\le 6[/latex]. There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.

Example: Solving a Compound Inequality

Solve the compound inequality: [latex]3\le 2x+2<6[/latex].

Answer: The first method is to write two separate inequalities: [latex]3\le 2x+2[/latex] and [latex]2x+2<6[/latex]. We solve them independently.

[latex]\begin{array}{lll}3\le 2x+2\hfill & \text{and}\hfill & 2x+2<6\hfill \\ 1\le 2x\hfill & \hfill & 2x<4\hfill \\ \frac{1}{2}\le x\hfill & \hfill & x<2\hfill \end{array}[/latex]
Then, we can rewrite the solution as a compound inequality, the same way the problem began.
[latex]\frac{1}{2}\le x<2[/latex]
In interval notation, the solution is written as [latex]\left[\frac{1}{2},2\right)[/latex]. The second method is to leave the compound inequality intact and perform solving procedures on the three parts at the same time.
[latex]\begin{array}{ll}3\le 2x+2<6\hfill & \hfill \\ 1\le 2x<4\hfill & \text{Isolate the variable term and subtract 2 from all three parts}.\hfill \\ \frac{1}{2}\le x<2\hfill & \text{Divide through all three parts by 2}.\hfill \end{array}[/latex]
We get the same solution: [latex]\left[\frac{1}{2},2\right)[/latex].

Try It

Solve the compound inequality [latex]4<2x - 8\le 10[/latex].

Answer: [latex]6<x\le 9\text{ }\text{ }\text{or}\left(6,9\right][/latex]

Example: Solving a Compound Inequality with the Variable in All Three Parts

Solve the compound inequality with variables in all three parts: [latex]3+x>7x - 2>5x - 10[/latex].

Answer: Let's try the first method. Write two inequalities:

[latex]\begin{array}{lll}3+x> 7x - 2\hfill & \text{and}\hfill & 7x - 2> 5x - 10\hfill \\ 3> 6x - 2\hfill & \hfill & 2x - 2> -10\hfill \\ 5> 6x\hfill & \hfill & 2x> -8\hfill \\ \frac{5}{6}> x\hfill & \hfill & x> -4\hfill \\ x< \frac{5}{6}\hfill & \hfill & -4< x\hfill \end{array}[/latex]
The solution set is [latex]-4<x<\frac{5}{6}[/latex] or in interval notation [latex]\left(-4,\frac{5}{6}\right)[/latex]. Notice that when we write the solution in interval notation, the smaller number comes first. We read intervals from left to right as they appear on a number line. A number line with the points -4 and 5/6 labeled. Dots appear at these points and a line connects these two dots.

Try It

Solve the compound inequality: [latex]3y<4 - 5y<5+3y[/latex].

Answer: [latex]\left(-\frac{1}{8},\frac{1}{2}\right)[/latex]

Solving Absolute Value Inequalities

As we know, the absolute value of a quantity is a positive number or zero. From the origin, a point located at [latex]\left(-x,0\right)[/latex] has an absolute value of [latex]x[/latex] as it is x units away. Consider absolute value as the distance from one point to another point. Regardless of direction, positive or negative, the distance between the two points is represented as a positive number or zero. An absolute value inequality is an equation of the form
[latex]|A|<B,|A|\le B,|A|>B,\text{or }|A|\ge B[/latex],
where A, and sometimes B, represents an algebraic expression dependent on a variable x. Solving the inequality means finding the set of all [latex]x[/latex] -values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values. There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph. Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of x-values such that the distance between [latex]x[/latex] and 600 is less than 200. We represent the distance between [latex]x[/latex] and 600 as [latex]|x - 600|[/latex], and therefore, [latex]|x - 600|\le 200[/latex] or
[latex]\begin{array}{c}-200\le x - 600\le 200\\ -200+600\le x - 600+600\le 200+600\\ 400\le x\le 800\end{array}[/latex]
This means our returns would be between $400 and $800. To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.

A General Note: Absolute Value Inequalities

For an algebraic expression X and [latex]k>0[/latex], an absolute value inequality is an inequality of the form:
[latex]\begin{array}{l}|X|< k\text{ which is equivalent to }-k< X< k\hfill \text{ or }\ |X|> k\text{ which is equivalent to }X< -k\text{ or }X> k\hfill \end{array}[/latex]
These statements also apply to [latex]|X|\le k[/latex] and [latex]|X|\ge k[/latex].

Example: Determining a Number within a Prescribed Distance

Describe all values [latex]x[/latex] within a distance of 4 from the number 5.

Answer: We want the distance between [latex]x[/latex] and 5 to be less than or equal to 4. We can draw a number line to represent the condition to be satisfied. A number line with one tick mark in the center labeled: 5. The tick marks on either side of the center one are not marked. Arrows extend from the center tick mark to the outer tick marks, both are labeled 4. The distance from [latex]x[/latex] to 5 can be represented using an absolute value symbol, [latex]|x - 5|[/latex]. Write the values of [latex]x[/latex] that satisfy the condition as an absolute value inequality.

[latex]|x - 5|\le 4[/latex]
We need to write two inequalities as there are always two solutions to an absolute value equation.
[latex]\begin{array}{lll}x - 5\le 4\hfill & \text{and}\hfill & x - 5\ge -4\hfill \\ x\le 9\hfill & \hfill & x\ge 1\hfill \end{array}[/latex]
If the solution set is [latex]x\le 9[/latex] and [latex]x\ge 1[/latex], then the solution set is an interval including all real numbers between and including 1 and 9. So [latex]|x - 5|\le 4[/latex] is equivalent to [latex]\left[1,9\right][/latex] in interval notation.

Try It

Describe all x-values within a distance of 3 from the number 2.

Answer: [latex]|x - 2|\le 3[/latex]

Example: Solving an Absolute Value Inequality

Solve [latex]|x - 1|\le 3[/latex].

Answer:

[latex]\begin{array}{c}|x - 1|\le 3\hfill \\ \hfill \\ -3\le x - 1\le 3\hfill \\ \hfill \\ -2\le x\le 4\hfill \\ \hfill \\ \left[-2,4\right]\hfill \end{array}[/latex]

Example: Using a Graphical Approach to Solve Absolute Value Inequalities

Given the equation [latex]y=-\frac{1}{2}|4x - 5|+3[/latex], determine the x-values for which the y-values are negative.

Answer: We are trying to determine where [latex]y<0[/latex] which is when [latex]-\frac{1}{2}|4x - 5|+3<0[/latex]. We begin by isolating the absolute value.

[latex]\begin{array}{ll}-\frac{1}{2}|4x - 5|< -3\hfill & \text{Multiply both sides by -2, and reverse the inequality}.\hfill \\ |4x - 5|> 6\hfill & \hfill \end{array}[/latex]
Next, we solve [latex]|4x - 5|=6[/latex].
[latex]\begin{array}{lll}4x - 5=6\hfill & \hfill & 4x - 5=-6\hfill \\ 4x=11\hfill & \text{or}\hfill & 4x=-1\hfill \\ x=\frac{11}{4}\hfill & \hfill & x=-\frac{1}{4}\hfill \end{array}[/latex]
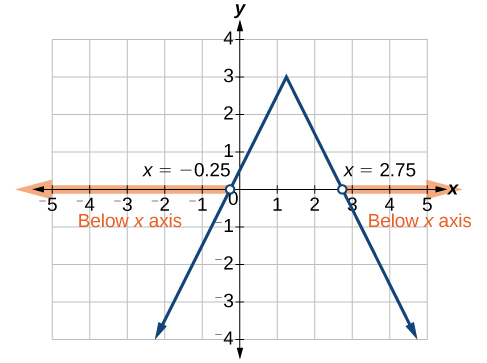
Now, we can examine the graph to observe where the y-values are negative. We observe where the branches are below the x-axis. Notice that it is not important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at [latex]x=-\frac{1}{4}[/latex] and [latex]x=\frac{11}{4}[/latex] and that the graph opens downward. A coordinate plan with the x-axis ranging from -5 to 5 and the y-axis ranging from -4 to 4. The function y = -1/2|4x – 5| + 3 is graphed. An open circle appears at the point -0.25 and an arrow

Try It

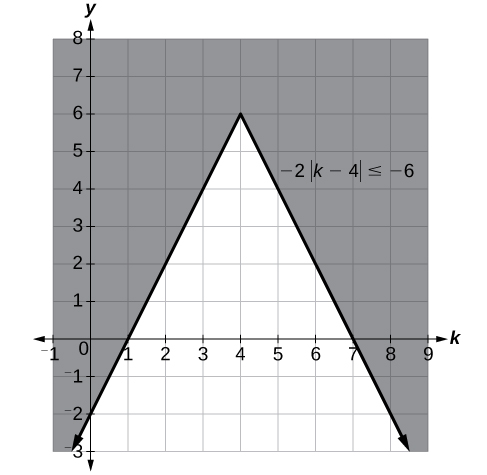
Solve [latex]-2|k - 4|\le -6[/latex].

Answer: [latex]k\le 1[/latex] or [latex]k\ge 7[/latex]; in interval notation, this would be [latex]\left(-\infty ,1\right]\cup \left[7,\infty \right)[/latex]. A coordinate plane with the x-axis ranging from -1 to 9 and the y-axis ranging from -3 to 8. The function y = -2|k 4| + 6 is graphed and everything above the function is shaded in.

Key Concepts

  • Interval notation is a method to give the solution set of an inequality. Highly applicable in calculus, it is a system of parentheses and brackets that indicate what numbers are included in a set and whether the endpoints are included as well.
  • Solving inequalities is similar to solving equations. The same algebraic rules apply, except for one: multiplying or dividing by a negative number reverses the inequality.
  • Compound inequalities often have three parts and can be rewritten as two independent inequalities. Solutions are given by boundary values which are indicated as a beginning boundary or an ending boundary in the solutions to the two inequalities.
  • Absolute value inequalities will produce two solution sets due to the nature of absolute value. We solve by writing two equations: one equal to a positive value and one equal to a negative value.
  • Absolute value inequality solutions can be verified by graphing. We can check the algebraic solutions by graphing as we cannot depend on a visual for a precise solution.

Glossary

compound inequality
a problem or a statement that includes two inequalities
interval
an interval describes a set of numbers where a solution falls
interval notation
a mathematical statement that describes a solution set and uses parentheses or brackets to indicate where an interval begins and ends
linear inequality
similar to a linear equation except that the solutions will include an interval of numbers

Licenses & Attributions

CC licensed content, Original

  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Graphing Inequalities. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/4529rytfef. License: CC BY: Attribution.

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 92604, 92605, 92606, 92607, 92608, 92609. Authored by: Michael Jenck. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 72891. Authored by: Alyson Day. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 58. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 89935. Authored by: Krystal Meier. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 15505. Authored by: Tophe Anderson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.