We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

TEXT
Unlock Solution Steps
Sign in to
Symbolab
Get full access to all Solution Steps for any math problem
By continuing, you agree to our Terms of Use
and have read our Privacy Policy

Study Guides > Calculus Volume 1

Substitution with Definite Integrals

Learning Objectives

  • Use substitution to evaluate definite integrals.

Substitution for Definite Integrals

Substitution can be used with definite integrals, too. However, using substitution to evaluate a definite integral requires a change to the limits of integration. If we change variables in the integrand, the limits of integration change as well.

Substitution with Definite Integrals

Let [latex]u=g(x)[/latex] and let [latex]{g}^{\text{′}}[/latex] be continuous over an interval [latex]\left[a,b\right],[/latex] and let [latex]f[/latex] be continuous over the range of [latex]u=g(x).[/latex] Then,

[latex]{\int }_{a}^{b}f(g(x)){g}^{\prime }(x)dx={\int }_{g(a)}^{g(b)}f(u)du.[/latex]

Although we will not formally prove this theorem, we justify it with some calculations here. From the substitution rule for indefinite integrals, if [latex]F(x)[/latex] is an antiderivative of [latex]f(x),[/latex] we have

[latex]\int f(g(x)){g}^{\prime }(x)dx=F(g(x))+C.[/latex]

Then

[latex]\begin{array}{cc}{\int }_{a}^{b}f\left[g(x)\right]{g}^{\prime }(x)dx\hfill & ={F(g(x))|}_{x=a}^{x=b}\hfill \\ & =F(g(b))-F(g(a))\hfill \\ & ={F(u)|}_{u=g(a)}^{u=g(b)}\hfill \\ \\ \\ & ={\int }_{g(a)}^{g(b)}f(u)du,\hfill \end{array}[/latex]

and we have the desired result.

Using Substitution to Evaluate a Definite Integral

Use substitution to evaluate [latex]{\int }_{0}^{1}{x}^{2}{(1+2{x}^{3})}^{5}dx.[/latex]

Answer:

Let [latex]u=1+2{x}^{3},[/latex] so [latex]du=6{x}^{2}dx.[/latex] Since the original function includes one factor of [latex]x[/latex]2 and [latex]du=6{x}^{2}dx,[/latex] multiply both sides of the du equation by [latex]1\text{/}6.[/latex] Then,

[latex]\begin{array}{ccc}du\hfill & =\hfill & 6{x}^{2}dx\hfill \\ \frac{1}{6}du\hfill & =\hfill & {x}^{2}dx.\hfill \end{array}[/latex]

To adjust the limits of integration, note that when [latex]x=0,u=1+2(0)=1,[/latex] and when [latex]x=1,u=1+2(1)=3.[/latex] Then

[latex]{\int }_{0}^{1}{x}^{2}{(1+2{x}^{3})}^{5}dx=\frac{1}{6}{\int }_{1}^{3}{u}^{5}du.[/latex]

Evaluating this expression, we get

[latex]\begin{array}{}\\ \\ \frac{1}{6}{\int }_{1}^{3}{u}^{5}du\hfill & =(\frac{1}{6})(\frac{{u}^{6}}{6}){|}_{1}^{3}\hfill \\ & =\frac{1}{36}\left[{(3)}^{6}-{(1)}^{6}\right]\hfill \\ & =\frac{182}{9}.\hfill \end{array}[/latex]

Use substitution to evaluate the definite integral [latex]{\int }_{-1}^{0}y{(2{y}^{2}-3)}^{5}dy.[/latex]

Answer:

[latex]\frac{91}{3}[/latex]

Using Substitution with an Exponential Function

Use substitution to evaluate [latex]{\int }_{0}^{1}x{e}^{4{x}^{2}+3}dx.[/latex]

Answer:

Let [latex]u=4{x}^{3}+3.[/latex] Then, [latex]du=8xdx.[/latex] To adjust the limits of integration, we note that when [latex]x=0,u=3,[/latex] and when [latex]x=1,u=7.[/latex] So our substitution gives

[latex]\begin{array}{cc}{\int }_{0}^{1}x{e}^{4{x}^{2}+3}dx\hfill & =\frac{1}{8}{\int }_{3}^{7}{e}^{u}du\hfill \\ \\ & =\frac{1}{8}{e}^{u}{|}_{3}^{7}\hfill \\ & =\frac{{e}^{7}-{e}^{3}}{8}\hfill \\ & \approx 134.568.\hfill \end{array}[/latex]

Use substitution to evaluate [latex]{\int }_{0}^{1}{x}^{2} \cos (\frac{\pi }{2}{x}^{3})dx.[/latex]

Answer:

[latex]\frac{2}{3\pi }\approx 0.2122[/latex]

Substitution may be only one of the techniques needed to evaluate a definite integral. All of the properties and rules of integration apply independently, and trigonometric functions may need to be rewritten using a trigonometric identity before we can apply substitution. Also, we have the option of replacing the original expression for [latex]u[/latex] after we find the antiderivative, which means that we do not have to change the limits of integration. These two approaches are shown in (Figure).

Using Substitution to Evaluate a Trigonometric Integral

Use substitution to evaluate [latex]{\int }_{0}^{\pi \text{/}2}{ \cos }^{2}\theta d\theta .[/latex]

Answer:

Let us first use a trigonometric identity to rewrite the integral. The trig identity [latex]{ \cos }^{2}\theta =\frac{1+ \cos 2\theta }{2}[/latex] allows us to rewrite the integral as

[latex]{\int }_{0}^{\pi \text{/}2}{ \cos }^{2}\theta d\theta ={\int }_{0}^{\pi \text{/}2}\frac{1+ \cos 2\theta }{2}d\theta .[/latex]

Then,

[latex]\begin{array}{cc}{\int }_{0}^{\pi \text{/}2}(\frac{1+ \cos 2\theta }{2})d\theta \hfill & ={\int }_{0}^{\pi \text{/}2}(\frac{1}{2}+\frac{1}{2} \cos 2\theta )d\theta \hfill \\ \\ \\ & =\frac{1}{2}{\int }_{0}^{\pi \text{/}2}d\theta +{\int }_{0}^{\pi \text{/}2} \cos 2\theta d\theta .\hfill \end{array}[/latex]

We can evaluate the first integral as it is, but we need to make a substitution to evaluate the second integral. Let [latex]u=2\theta .[/latex] Then, [latex]du=2d\theta ,[/latex] or [latex]\frac{1}{2}du=d\theta .[/latex] Also, when [latex]\theta =0,u=0,[/latex] and when [latex]\theta =\pi \text{/}2,u=\pi .[/latex] Expressing the second integral in terms of [latex]u[/latex], we have

[latex]\begin{array}{}\\ \\ \frac{1}{2}{\int }_{0}^{\pi \text{/}2}d\theta +\frac{1}{2}{\int }_{0}^{\pi \text{/}2} \cos 2\theta d\theta \hfill & =\frac{1}{2}{\int }_{0}^{\pi \text{/}2}d\theta +\frac{1}{2}(\frac{1}{2}){\int }_{0}^{\pi } \cos udu\hfill \\ & =\frac{\theta }{2}{|}_{\theta =0}^{\theta =\pi \text{/}2}+\frac{1}{4} \sin u{|}_{u=0}^{u=\theta }\hfill \\ & =(\frac{\pi }{4}-0)+(0-0)=\frac{\pi }{4}.\hfill \end{array}[/latex]

Evaluating a Definite Integral Involving an Exponential Function

Evaluate the definite integral [latex]{\int }_{1}^{2}{e}^{1-x}dx.[/latex]

Answer:

Again, substitution is the method to use. Let [latex]u=1-x,[/latex] so [latex]du=-1dx[/latex] or [latex]\text{−}du=dx.[/latex] Then [latex]\int {e}^{1-x}dx=\text{−}\int {e}^{u}du.[/latex] Next, change the limits of integration. Using the equation [latex]u=1-x,[/latex] we have

[latex]\begin{array}{c}u=1-(1)=0\hfill \\ u=1-(2)=-1.\hfill \end{array}[/latex]

The integral then becomes

[latex]\begin{array}{cc}{\int }_{1}^{2}{e}^{1-x}dx\hfill & =\text{−}{\int }_{0}^{-1}{e}^{u}du\hfill \\ \\ \\ & ={\int }_{-1}^{0}{e}^{u}du\hfill \\ & ={{e}^{u}|}_{-1}^{0}\hfill \\ & ={e}^{0}-({e}^{-1})\hfill \\ & =\text{−}{e}^{-1}+1.\hfill \end{array}[/latex]

See (Figure).

A graph of the function f(x) = e^(1-x) over [0, 3]. It crosses the y axis at (0, e) as a decreasing concave up curve and symptotically approaches 0 as x goes to infinity. Figure 2. The indicated area can be calculated by evaluating a definite integral using substitution.

Evaluate [latex]{\int }_{0}^{2}{e}^{2x}dx.[/latex]

Answer:

[latex]\frac{1}{2}{\int }_{0}^{4}{e}^{u}du=\frac{1}{2}({e}^{4}-1)[/latex]

Hint

Let [latex]u=2x.[/latex]

Evaluating a Definite Integral Using Substitution

Evaluate the definite integral using substitution: [latex]{\int }_{1}^{2}\frac{{e}^{1\text{/}x}}{{x}^{2}}dx.[/latex]

Answer:

This problem requires some rewriting to simplify applying the properties. First, rewrite the exponent on [latex]e[/latex] as a power of [latex]x[/latex], then bring the [latex]x[/latex]2 in the denominator up to the numerator using a negative exponent. We have

[latex]{\int }_{1}^{2}\frac{{e}^{1\text{/}x}}{{x}^{2}}dx={\int }_{1}^{2}{e}^{{x}^{-1}}{x}^{-2}dx.[/latex]

Let [latex]u={x}^{-1},[/latex] the exponent on [latex]e[/latex]. Then

[latex]\begin{array}{cc}\hfill du& =\text{−}{x}^{-2}dx\hfill \\ \hfill -du& ={x}^{-2}dx.\hfill \end{array}[/latex]

Bringing the negative sign outside the integral sign, the problem now reads

[latex]\text{−}\int {e}^{u}du.[/latex]

Next, change the limits of integration:

[latex]\begin{array}{}\\ \\ u={(1)}^{-1}=1\hfill \\ u={(2)}^{-1}=\frac{1}{2}.\hfill \end{array}[/latex]
Notice that now the limits begin with the larger number, meaning we must multiply by −1 and interchange the limits. Thus,
[latex]\begin{array}{}\\ \\ \\ \text{−}{\int }_{1}^{1\text{/}2}{e}^{u}du\hfill & ={\int }_{1\text{/}2}^{1}{e}^{u}du\hfill \\ & ={e}^{u}{|}_{1\text{/}2}^{1}\hfill \\ & =e-{e}^{1\text{/}2}\hfill \\ & =e-\sqrt{e}.\hfill \end{array}[/latex]

Evaluate the definite integral using substitution: [latex]{\int }_{1}^{2}\frac{1}{{x}^{3}}{e}^{4{x}^{-2}}dx.[/latex]

Answer:

[latex]{\int }_{1}^{2}\frac{1}{{x}^{3}}{e}^{4{x}^{-2}}dx=\frac{1}{8}\left[{e}^{4}-e\right][/latex]

Hint

Let [latex]u=4{x}^{-2}.[/latex]

(Figure) is a definite integral of a trigonometric function. With trigonometric functions, we often have to apply a trigonometric property or an identity before we can move forward. Finding the right form of the integrand is usually the key to a smooth integration.

Evaluating a Definite Integral

Find the definite integral of [latex]{\int }_{0}^{\pi \text{/}2}\frac{ \sin x}{1+ \cos x}dx.[/latex]

Answer:

We need substitution to evaluate this problem. Let [latex]u=1+ \cos x,,[/latex] so [latex]du=\text{−} \sin xdx.[/latex] Rewrite the integral in terms of [latex]u[/latex], changing the limits of integration as well. Thus,

[latex]\begin{array}{c}u=1+ \cos (0)=2\hfill \\ u=1+ \cos (\frac{\pi }{2})=1.\hfill \end{array}[/latex]

Then

[latex]\begin{array}{cc}{\int }_{0}^{\pi \text{/}2}\frac{ \sin x}{1+ \cos x}\hfill & =\text{−}{\int }_{2}^{1}{u}^{-1}du\hfill \\ \\ \\ & ={\int }_{1}^{2}{u}^{-1}du\hfill \\ & ={\text{ln}|u||}_{1}^{2}\hfill \\ & =\left[\text{ln}2-\text{ln}1\right]\hfill \\ & =\text{ln}2.\hfill \end{array}[/latex]

Evaluating a Definite Integral Using Inverse Trigonometric Functions

Evaluate the definite integral [latex]{\int }_{0}^{1}\frac{dx}{\sqrt{1-{x}^{2}}}.[/latex]

Answer: We can go directly to the formula for the antiderivative in the rule on integration formulas resulting in inverse trigonometric functions, and then evaluate the definite integral. We have

[latex]\begin{array}{}\\ \\ {\int }_{0}^{1}\frac{dx}{\sqrt{1-{x}^{2}}}\hfill & ={ \sin }^{-1}x{|}_{0}^{1}\hfill \\ & ={ \sin }^{-1}1-{ \sin }^{-1}0\hfill \\ & =\frac{\pi }{2}-0\hfill \\ & =\frac{\pi }{2}.\hfill \end{array}[/latex]

Evaluating a Definite Integral

Evaluate the definite integral [latex]{\int }_{0}^{\sqrt{3}\text{/}2}\frac{du}{\sqrt{1-{u}^{2}}}.[/latex]

Answer:

The format of the problem matches the inverse sine formula. Thus,

[latex]\begin{array}{}\\ \\ {\int }_{0}^{\sqrt{3}\text{/}2}\frac{du}{\sqrt{1-{u}^{2}}}\hfill & ={ \sin }^{-1}u{|}_{0}^{\sqrt{3}\text{/}2}\hfill \\ & =\left[{ \sin }^{-1}(\frac{\sqrt{3}}{2})\right]-\left[{ \sin }^{-1}(0)\right]\hfill \\ & =\frac{\pi }{3}.\hfill \end{array}[/latex]

Evaluating a Definite Integral

Evaluate the definite integral [latex]{\int }_{\sqrt{3}\text{/}3}^{\sqrt{3}}\frac{dx}{1+{x}^{2}}.[/latex]

Answer:

Use the formula for the inverse tangent. We have

[latex]\begin{array}{}\\ \\ {\int }_{\sqrt{3}\text{/}3}^{\sqrt{3}}\frac{dx}{1+{x}^{2}}\hfill & ={ \tan }^{-1}x{|}_{\sqrt{3}\text{/}3}^{\sqrt{3}}\hfill \\ & =\left[{ \tan }^{-1}(\sqrt{3})\right]-\left[{ \tan }^{-1}(\frac{\sqrt{3}}{3})\right]\hfill \\ & =\frac{\pi }{6}.\hfill \end{array}[/latex]

Evaluate the definite integral [latex]{\int }_{0}^{2}\frac{dx}{4+{x}^{2}}.[/latex]

Answer:

[latex]\frac{\pi }{8}[/latex]

Hint

Follow the procedures from (Figure) to solve the problem.

In the following exercises, use a calculator to estimate the area under the curve using left Riemann sums with 50 terms, then use substitution to solve for the exact answer.

1. [T][latex]y=3{(1-x)}^{2}[/latex] over [latex]\left[0,2\right][/latex]

2. [T][latex]y=x{(1-{x}^{2})}^{3}[/latex] over [latex]\left[-1,2\right][/latex]

Answer:

[latex]{L}_{50}=-8.5779.[/latex] The exact area is [latex]\frac{-81}{8}[/latex]

3. [T][latex]y= \sin x{(1- \cos x)}^{2}[/latex] over [latex]\left[0,\pi \right][/latex]

4. [T][latex]y=\frac{x}{{({x}^{2}+1)}^{2}}[/latex] over [latex]\left[-1,1\right][/latex]

Answer:

[latex]{L}_{50}=-0.006399[/latex] … The exact area is 0.

In the following exercises, use a change of variables to evaluate the definite integral.

5. [latex]{\int }_{0}^{1}x\sqrt{1-{x}^{2}}dx[/latex]

6. [latex]{\int }_{0}^{1}\frac{x}{\sqrt{1+{x}^{2}}}dx[/latex]

Answer:

[latex]u=1+{x}^{2},du=2xdx,\frac{1}{2}{\int }_{1}^{2}{u}^{-1\text{/}2}du=\sqrt{2}-1[/latex]

7. [latex]{\int }_{0}^{2}\frac{t}{\sqrt{5+{t}^{2}}}dt[/latex]

8. [latex]{\int }_{0}^{1}\frac{t}{\sqrt{1+{t}^{3}}}dt[/latex]

Answer:

[latex]u=1+{t}^{3},du=3{t}^{2},\frac{1}{3}{\int }_{1}^{2}{u}^{-1\text{/}2}du=\frac{2}{3}(\sqrt{2}-1)[/latex]

9. [latex]{\int }_{0}^{\pi \text{/}4}{ \sec }^{2}\theta \tan \theta d\theta [/latex]

10. [latex]{\int }_{0}^{\pi \text{/}4}\frac{ \sin \theta }{{ \cos }^{4}\theta }d\theta [/latex]

Answer:

[latex]u= \cos \theta ,du=\text{−} \sin \theta d\theta ,{\int }_{1\text{/}\sqrt{2}}^{1}{u}^{-4}du=\frac{1}{3}(2\sqrt{2}-1)[/latex]

In the following exercises, evaluate the indefinite integral [latex]\int f(x)dx[/latex] with constant [latex]C=0[/latex] using [latex]u[/latex]-substitution. Then, graph the function and the antiderivative over the indicated interval. If possible, estimate a value of C that would need to be added to the antiderivative to make it equal to the definite integral [latex]F(x)={\int }_{a}^{x}f(t)dt,[/latex] with [latex]a[/latex] the left endpoint of the given interval.

11. [T][latex]\int (2x+1){e}^{{x}^{2}+x-6}dx[/latex] over [latex]\left[-3,2\right][/latex]

12. [T][latex]\int \frac{ \cos (\text{ln}(2x))}{x}dx[/latex] on [latex]\left[0,2\right][/latex]

Answer:

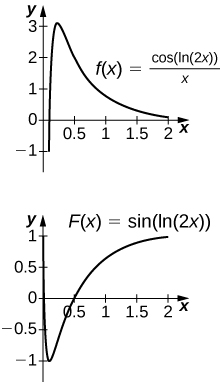Two graphs. The first shows the function f(x) = cos(ln(2x)) / x, which increases sharply over the approximate interval (0,.25) and then decreases gradually to the x axis. The second shows the function f(x) = sin(ln(2x)), which decreases sharply on the approximate interval (0, .25) and then increases in a gently curve into the first quadrant. The antiderivative is [latex]y= \sin (\text{ln}(2x)).[/latex] Since the antiderivative is not continuous at [latex]x=0,[/latex] one cannot find a value of C that would make [latex]y= \sin (\text{ln}(2x))-C[/latex] work as a definite integral. 

13. [T][latex]\int \frac{3{x}^{2}+2x+1}{\sqrt{{x}^{3}+{x}^{2}+x+4}}dx[/latex] over [latex]\left[-1,2\right][/latex]

14. [T][latex]\int \frac{ \sin x}{{ \cos }^{3}x}dx[/latex] over [latex]\left[-\frac{\pi }{3},\frac{\pi }{3}\right][/latex]

Answer:

Two graphs. The first is the function f(x) = sin(x) / cos(x)^3 over [-5pi/16, 5pi/16]. It is an increasing concave down function for values less than zero and an increasing concave up function for values greater than zero. The second is the fuction f(x) = ½ sec(x)^2 over the same interval. It is a wide, concave up curve which decreases for values less than zero and increases for values greater than zero. The antiderivative is [latex]y=\frac{1}{2}\phantom{\rule{0.05em}{0ex}}{ \sec }^{2}x.[/latex] You should take [latex]C=-2[/latex] so that [latex]F(-\frac{\pi }{3})=0.[/latex]

15. [T][latex]\int (x+2){e}^{\text{−}{x}^{2}-4x+3}dx[/latex] over [latex]\left[-5,1\right][/latex]

16. [T][latex]\int 3{x}^{2}\sqrt{2{x}^{3}+1}dx[/latex] over [latex]\left[0,1\right][/latex]

Answer:

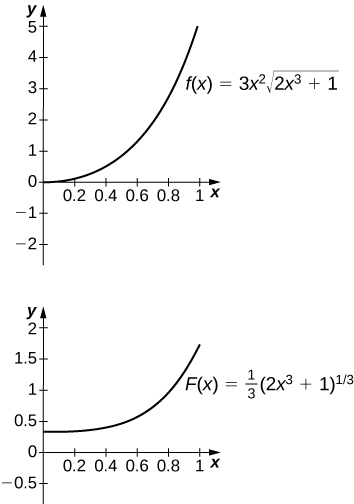Two graphs. The first shows the function f(x) = 3x^2 * sqrt(2x^3 + 1). It is an increasing concave up curve starting at the origin. The second shows the function f(x) = 1/3 * (2x^3 + 1)^(1/3). It is an increasing concave up curve starting at about 0.3. The antiderivative is [latex]y=\frac{1}{3}{(2{x}^{3}+1)}^{3\text{/}2}.[/latex] One should take [latex]C=-\frac{1}{3}.[/latex]

17. If [latex]h(a)=h(b)[/latex] in [latex]{\int }_{a}^{b}g\text{‘}(h(x))h(x)dx,[/latex] what can you say about the value of the integral?

18. Is the substitution [latex]u=1-{x}^{2}[/latex] in the definite integral [latex]{\int }_{0}^{2}\frac{x}{1-{x}^{2}}dx[/latex] okay? If not, why not?

Answer:

No, because the integrand is discontinuous at [latex]x=1.[/latex]

In the following exercises, use a change of variables to show that each definite integral is equal to zero.

19. [latex]{\int }_{0}^{\pi }{ \cos }^{2}(2\theta ) \sin (2\theta )d\theta [/latex]

20. [latex]{\int }_{0}^{\sqrt{\pi }}t \cos ({t}^{2}) \sin ({t}^{2})dt[/latex]

Answer:

[latex]u= \sin ({t}^{2});[/latex] the integral becomes [latex]\frac{1}{2}{\int }_{0}^{0}udu.[/latex]

21. [latex]{\int }_{0}^{1}(1-2t)dt[/latex]

22. [latex]{\int }_{0}^{1}\frac{1-2t}{(1+{(t-\frac{1}{2})}^{2})}dt[/latex]

Answer:

[latex]u=(1+{(t-\frac{1}{2})}^{2});[/latex] the integral becomes [latex]\text{−}{\int }_{5\text{/}4}^{5\text{/}4}\frac{1}{u}du.[/latex]

23. [latex]{\int }_{0}^{\pi } \sin ({(t-\frac{\pi }{2})}^{3}) \cos (t-\frac{\pi }{2})dt[/latex]

24. [latex]{\int }_{0}^{2}(1-t) \cos (\pi t)dt[/latex]

Answer:

[latex]u=1-t;[/latex] the integral becomes

[latex-display]\begin{array}{l}{\int }_{1}^{-1}u \cos (\pi (1-u))du\hfill \\ ={\int }_{1}^{-1}u\left[ \cos \pi \cos u- \sin \pi \sin u\right]du\hfill \\ =\text{−}{\int }_{1}^{-1}u \cos udu\hfill \\ ={\int }_{-1}^{1}u \cos udu=0\hfill \end{array}[/latex-display] since the integrand is odd.

25. [latex]{\int }_{\pi \text{/}4}^{3\pi \text{/}4}{ \sin }^{2}t \cos tdt[/latex]

26. Show that the average value of [latex]f(x)[/latex] over an interval [latex]\left[a,b\right][/latex] is the same as the average value of [latex]f(cx)[/latex] over the interval [latex]\left[\frac{a}{c},\frac{b}{c}\right][/latex] for [latex]c>0.[/latex]

Answer:

Setting [latex]u=cx[/latex] and [latex]du=cdx[/latex] gets you [latex]\frac{1}{\frac{b}{c}-\frac{a}{c}}{\int }_{a\text{/}c}^{b\text{/}c}f(cx)dx=\frac{c}{b-a}{\int }_{u=a}^{u=b}f(u)\frac{du}{c}=\frac{1}{b-a}{\int }_{a}^{b}f(u)du.[/latex]

27. Find the area under the graph of [latex]f(t)=\frac{t}{{(1+{t}^{2})}^{a}}[/latex] between [latex]t=0[/latex] and [latex]t=x[/latex] where [latex]a>0[/latex] and [latex]a\ne 1[/latex] is fixed, and evaluate the limit as [latex]x\to \infty .[/latex]

28. Find the area under the graph of [latex]g(t)=\frac{t}{{(1-{t}^{2})}^{a}}[/latex] between [latex]t=0[/latex] and [latex]t=x,[/latex] where [latex]0<x<1[/latex] and [latex]a>0[/latex] is fixed. Evaluate the limit as [latex]x\to 1.[/latex]

Answer:

[latex]{\int }_{0}^{x}g(t)dt=\frac{1}{2}{\int }_{u=1-{x}^{2}}^{1}\frac{du}{{u}^{a}}=\frac{1}{2(1-a)}{u}^{1-a}{|}_{u=1-{x}^{2}}^{1}=\frac{1}{2(1-a)}(1-{(1-{x}^{2})}^{1-a}).[/latex] As [latex]x\to 1[/latex] the limit is [latex]\frac{1}{2(1-a)}[/latex] if [latex]a<1,[/latex] and the limit diverges to +∞ if [latex]a>1.[/latex]

29. The area of a semicircle of radius 1 can be expressed as [latex]{\int }_{-1}^{1}\sqrt{1-{x}^{2}}dx.[/latex] Use the substitution [latex]x= \cos t[/latex] to express the area of a semicircle as the integral of a trigonometric function. You do not need to compute the integral.

30. The area of the top half of an ellipse with a major axis that is the [latex]x[/latex]-axis from [latex]x=-1[/latex] to [latex]a[/latex] and with a minor axis that is the [latex]y[/latex]-axis from [latex]y=\text{−}b[/latex] to [latex]b[/latex] can be written as [latex]{\int }_{\text{−}a}^{a}b\sqrt{1-\frac{{x}^{2}}{{a}^{2}}}dx.[/latex] Use the substitution [latex]x=a \cos t[/latex] to express this area in terms of an integral of a trigonometric function. You do not need to compute the integral.

Answer:

[latex]{\int }_{t=\pi }^{0}b\sqrt{1-{ \cos }^{2}t}×(\text{−}a \sin t)dt={\int }_{t=0}^{\pi }ab{ \sin }^{2}tdt[/latex]

31. [T] The following graph is of a function of the form [latex]f(t)=a \sin (nt)+b \sin (mt).[/latex] Estimate the coefficients [latex]a[/latex] and [latex]b[/latex], and the frequency parameters [latex]n[/latex] and [latex]m[/latex]. Use these estimates to approximate [latex]{\int }_{0}^{\pi }f(t)dt.[/latex]

A graph of a function of the given form over [0, 2pi], which has six turning points. They are located at just before pi/4, just after pi/2, between 3pi/4 and pi, between pi and 5pi/4, just before 3pi/2, and just after 7pi/4 at about 3, -2, 1, -1, 2, and -3. It begins at the origin and ends at (2pi, 0). It crosses the x axis between pi/4 and pi/2, just before 3pi/4, pi, just after 5pi/4, and between 3pi/2 and 4pi/4.

32. [T] The following graph is of a function of the form [latex]f(x)=a \cos (nt)+b \cos (mt).[/latex] Estimate the coefficients [latex]a[/latex] and [latex]b[/latex] and the frequency parameters [latex]n[/latex] and [latex]m[/latex]. Use these estimates to approximate [latex]{\int }_{0}^{\pi }f(t)dt.[/latex]

The graph of a function of the given form over [0, 2pi]. It begins at (0,1) and ends at (2pi, 1). It has five turning points, located just after pi/4, between pi/2 and 3pi/4, pi, between 5pi/4 and 3pi/2, and just before 7pi/4 at about -1.5, 2.5, -3, 2.5, and -1. It crosses the x axis between 0 and pi/4, just before pi/2, just after 3pi/4, just before 5pi/4, just after 3pi/2, and between 7pi/4 and 2pi.

Answer:

[latex]f(t)=2 \cos (3t)- \cos (2t);{\int }_{0}^{\pi \text{/}2}(2 \cos (3t)- \cos (2t))=-\frac{2}{3}[/latex]

33. [latex]{\int }_{0}^{\pi \text{/}4} \tan xdx[/latex]

34. [latex]{\int }_{0}^{\pi \text{/}3}\frac{ \sin x- \cos x}{ \sin x+ \cos x}dx[/latex]

Answer:

[latex]\text{ln}(\sqrt{3}-1)[/latex]

35. [latex]{\int }_{\pi \text{/}6}^{\pi \text{/}2} \csc xdx[/latex]

36. [latex]{\int }_{\pi \text{/}4}^{\pi \text{/}3} \cot xdx[/latex]

Answer:

[latex]\frac{1}{2}\text{ln}\frac{3}{2}[/latex]

In the following exercises, does the right-endpoint approximation overestimate or underestimate the exact area? Calculate the right endpoint estimate R50 and solve for the exact area.

37. [T][latex]y={e}^{x}[/latex] over [latex]\left[0,1\right][/latex]

38. [T][latex]y={e}^{\text{−}x}[/latex] over [latex]\left[0,1\right][/latex]

Answer:

Exact solution: [latex]\frac{e-1}{e},{R}_{50}=0.6258.[/latex] Since [latex]f[/latex] is decreasing, the right endpoint estimate underestimates the area.

39. [T][latex]y=\text{ln}(x)[/latex] over [latex]\left[1,2\right][/latex]

40. [T][latex]y=\frac{x+1}{{x}^{2}+2x+6}[/latex] over [latex]\left[0,1\right][/latex]

Answer:

Exact solution: [latex]\frac{2\text{ln}(3)-\text{ln}(6)}{2},{R}_{50}=0.2033.[/latex] Since [latex]f[/latex] is increasing, the right endpoint estimate overestimates the area.

41. [T][latex]y={2}^{x}[/latex] over [latex]\left[-1,0\right][/latex]

42. [T][latex]y=\text{−}{2}^{\text{−}x}[/latex] over [latex]\left[0,1\right][/latex]

Answer:

Exact solution: [latex]-\frac{1}{\text{ln}(4)},{R}_{50}=-0.7164.[/latex] Since [latex]f[/latex] is increasing, the right endpoint estimate overestimates the area (the actual area is a larger negative number).

In the following exercises, [latex]f(x)\ge 0[/latex] for [latex]a\le x\le b.[/latex] Find the area under the graph of [latex]f(x)[/latex] between the given values [latex]a[/latex] and [latex]b[/latex] by integrating.

43. [latex]f(x)=\frac{{\text{log}}_{10}(x)}{x};a=10,b=100[/latex]

44. [latex]f(x)=\frac{{\text{log}}_{2}(x)}{x};a=32,b=64[/latex]

Answer:

[latex]\frac{11}{2}\text{ln}2[/latex]

45. [latex]f(x)={2}^{\text{−}x};a=1,b=2[/latex]

46. [latex]f(x)={2}^{\text{−}x};a=3,b=4[/latex]

Answer:

[latex]\frac{1}{\text{ln}(65,536)}[/latex]

47. Find the area under the graph of the function [latex]f(x)=x{e}^{\text{−}{x}^{2}}[/latex] between [latex]x=0[/latex] and [latex]x=5.[/latex]

48. Compute the integral of [latex]f(x)=x{e}^{\text{−}{x}^{2}}[/latex] and find the smallest value of N such that the area under the graph [latex]f(x)=x{e}^{\text{−}{x}^{2}}[/latex] between [latex]x=N[/latex] and [latex]x=N+10[/latex] is, at most, 0.01.

Answer: [latex]{\int }_{N}^{N+1}x{e}^{\text{−}{x}^{2}}dx=\frac{1}{2}({e}^{\text{−}{N}^{2}}-{e}^{\text{−}{(N+1)}^{2}}).[/latex] The quantity is less than 0.01 when [latex]N=2.[/latex]

49. Find the limit, as N tends to infinity, of the area under the graph of [latex]f(x)=x{e}^{\text{−}{x}^{2}}[/latex] between [latex]x=0[/latex] and [latex]x=5.[/latex]

50. Show that [latex]{\int }_{a}^{b}\frac{dt}{t}={\int }_{1\text{/}b}^{1\text{/}a}\frac{dt}{t}[/latex] when [latex]0<a\le b.[/latex]

Answer:

[latex]{\int }_{a}^{b}\frac{dx}{x}=\text{ln}(b)-\text{ln}(a)=\text{ln}(\frac{1}{a})-\text{ln}(\frac{1}{b})={\int }_{1\text{/}b}^{1\text{/}a}\frac{dx}{x}[/latex]

51. Suppose that [latex]f(x)>0[/latex] for all [latex]x[/latex] and that [latex]f[/latex] and [latex]g[/latex] are differentiable. Use the identity [latex]{f}^{g}={e}^{g\text{ln}f}[/latex] and the chain rule to find the derivative of [latex]{f}^{g}.[/latex]

52. Use the previous exercise to find the antiderivative of [latex]h(x)={x}^{x}(1+\text{ln}x)[/latex] and evaluate [latex]{\int }_{2}^{3}{x}^{x}(1+\text{ln}x)dx.[/latex]

Answer:

23

53. Show that if [latex]c>0,[/latex] then the integral of [latex]1\text{/}x[/latex] from ac to bc [latex](0<a<b)[/latex] is the same as the integral of [latex]1\text{/}x[/latex] from [latex]a[/latex] to [latex]b[/latex].

The following exercises are intended to derive the fundamental properties of the natural log starting from the Definition/em> [latex]\text{ln}(x)={\int }_{1}^{x}\frac{dt}{t},[/latex] using properties of the definite integral and making no further assumptions.

54. Use the identity [latex]\text{ln}(x)={\int }_{1}^{x}\frac{dt}{t}[/latex] to derive the identity [latex]\text{ln}(\frac{1}{x})=\text{−}\text{ln}x.[/latex]

Answer:

We may assume that [latex]x>1,\text{so}\frac{1}{x}<1.[/latex] Then, [latex]{\int }_{1}^{1\text{/}x}\frac{dt}{t}.[/latex] Now make the substitution [latex]u=\frac{1}{t},[/latex] so [latex]du=-\frac{dt}{{t}^{2}}[/latex] and [latex]\frac{du}{u}=-\frac{dt}{t},[/latex] and change endpoints: [latex]{\int }_{1}^{1\text{/}x}\frac{dt}{t}=\text{−}{\int }_{1}^{x}\frac{du}{u}=\text{−}\text{ln}x.[/latex]

55. Use a change of variable in the integral [latex]{\int }_{1}^{xy}\frac{1}{t}dt[/latex] to show that [latex]\text{ln}xy=\text{ln}x+\text{ln}y\text{ for }x,y>0.[/latex]

56. Use the identity [latex]\text{ln}x={\int }_{1}^{x}\frac{dt}{x}[/latex] to show that [latex]\text{ln}(x)[/latex] is an increasing function of [latex]x[/latex] on [latex][0,\infty )[/latex] and use the previous exercises to show that the range of [latex]\text{ln}(x)[/latex] is [latex](\text{−}\infty ,\infty ).[/latex] Without any further assumptions, conclude that [latex]\text{ln}(x)[/latex] has an inverse function defined on [latex](\text{−}\infty ,\infty ).[/latex]

57. Pretend, for the moment, that we do not know that [latex]{e}^{x}[/latex] is the inverse function of [latex]\text{ln}(x),[/latex] but keep in mind that [latex]\text{ln}(x)[/latex] has an inverse function defined on [latex](\text{−}\infty ,\infty ).[/latex] Call it E. Use the identity [latex]\text{ln}xy=\text{ln}x+\text{ln}y[/latex] to deduce that [latex]E(a+b)=E(a)E(b)[/latex] for any real numbers [latex]a[/latex], [latex]b[/latex].

58. Pretend, for the moment, that we do not know that [latex]{e}^{x}[/latex] is the inverse function of [latex]\text{ln}x,[/latex] but keep in mind that [latex]\text{ln}x[/latex] has an inverse function defined on [latex](\text{−}\infty ,\infty ).[/latex] Call it E. Show that [latex]E\text{'}(t)=E(t).[/latex]

Answer:

[latex]x=E(\text{ln}(x)).[/latex] Then, [latex]1=\frac{E\text{'}(\text{ln}x)}{x}\text{or}x=E\text{'}(\text{ln}x).[/latex] Since any number [latex]t[/latex] can be written [latex]t=\text{ln}x[/latex] for some [latex]x[/latex], and for such [latex]t[/latex] we have [latex]x=E(t),[/latex] it follows that for any [latex]t,E\text{'}(t)=E(t).[/latex]

59. The sine integral, defined as [latex]S(x)={\int }_{0}^{x}\frac{ \sin t}{t}dt[/latex] is an important quantity in engineering. Although it does not have a simple closed formula, it is possible to estimate its behavior for large [latex]x[/latex]. Show that for [latex]k\ge 1,|S(2\pi k)-S(2\pi (k+1))|\le \frac{1}{k(2k+1)\pi }.[/latex](Hint: [latex]\sin (t+\pi )=\text{−} \sin t[/latex])

60. [T] The normal distribution in probability is given by [latex]p(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\text{−}{(x-\mu )}^{2}\text{/}2{\sigma }^{2}},[/latex] where σ is the standard deviation and μ is the average. The standard normal distribution in probability, [latex]{p}_{s},[/latex] corresponds to [latex]\mu =0\text{ and }\sigma =1.[/latex] Compute the left endpoint estimates [latex]{R}_{10}\text{ and }{R}_{100}[/latex] of [latex]{\int }_{-1}^{1}\frac{1}{\sqrt{2\pi }}{e}^{\text{−}{x}^{2\text{/}2}}dx.[/latex]

Answer:

[latex]{R}_{10}=0.6811,{R}_{100}=0.6827[/latex]

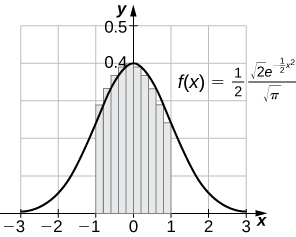
A graph of the function f(x) = .5 * ( sqrt(2)*e^(-.5x^2)) / sqrt(pi). It is a downward opening curve that is symmetric across the y axis, crossing at about (0, .4). It approaches 0 as x goes to positive and negative infinity. Between 1 and -1, ten rectangles are drawn for a right endpoint estimate of the area under the curve.

61. [T] Compute the right endpoint estimates [latex]{R}_{50}\text{ and }{R}_{100}[/latex] of [latex]{\int }_{-3}^{5}\frac{1}{2\sqrt{2\pi }}{e}^{\text{−}{(x-1)}^{2}\text{/}8}.[/latex]

In the following exercises, evaluate each integral in terms of an inverse trigonometric function.

62. [latex]{\int }_{0}^{\sqrt{3}\text{/}2}\frac{dx}{\sqrt{1-{x}^{2}}}[/latex]

Answer:

[latex]{ \sin }^{-1}x{|}_{0}^{\sqrt{3}\text{/}2}=\frac{\pi }{3}[/latex]

63. [latex]{\int }_{-1\text{/}2}^{1\text{/}2}\frac{dx}{\sqrt{1-{x}^{2}}}[/latex]

64. [latex]{\int }_{\sqrt{3}}^{1}\frac{dx}{\sqrt{1+{x}^{2}}}[/latex]

Answer:

[latex]{ \tan }^{-1}x{|}_{\sqrt{3}}^{1}=-\frac{\pi }{12}[/latex]

65. [latex]{\int }_{1\text{/}\sqrt{3}}^{\sqrt{3}}\frac{dx}{1+{x}^{2}}[/latex]

66. [latex]{\int }_{1}^{\sqrt{2}}\frac{dx}{|x|\sqrt{{x}^{2}-1}}[/latex]

Answer:

[latex]{ \sec }^{-1}x{|}_{1}^{\sqrt{2}}=\frac{\pi }{4}[/latex]

67. [latex]{\int }_{1}^{2\text{/}\sqrt{3}}\frac{dx}{|x|\sqrt{{x}^{2}-1}}[/latex]

68. Explain what is wrong with the following integral: [latex]{\int }_{1}^{2}\frac{dt}{\sqrt{1-{t}^{2}}}.[/latex]

Answer:

[latex]\sqrt{1-{t}^{2}}[/latex] is not defined as a real number when [latex]t>1.[/latex]

69. Explain what is wrong with the following integral: [latex]{\int }_{-1}^{1}\frac{dt}{|t|\sqrt{{t}^{2}-1}}.[/latex]

In the following exercises, solve for the antiderivative [latex]\int f[/latex] of [latex]f[/latex] with [latex]C=0,[/latex] then use a calculator to graph [latex]f[/latex] and the antiderivative over the given interval [latex]\left[a,b\right].[/latex] Identify a value of C such that adding C to the antiderivative recovers the definite integral [latex]F(x)={\int }_{a}^{x}f(t)dt.[/latex]

70. [T][latex]\int \frac{1}{\sqrt{9-{x}^{2}}}dx[/latex] over [latex]\left[-3,3\right][/latex]

Answer: Two graphs. The first shows the function f(x) = 1 / sqrt(9 – x^2). It is an upward opening curve symmetric about the y axis, crossing at (0, 1/3). The second shows the function F(x) = arcsin(1/3 x). It is an increasing curve going through the origin. The antiderivative is [latex]{ \sin }^{-1}(\frac{x}{3})+C.[/latex] Taking [latex]C=\frac{\pi }{2}[/latex] recovers the definite integral.

71. [T][latex]\int \frac{9}{9+{x}^{2}}dx[/latex] over [latex]\left[-6,6\right][/latex]

72. [T][latex]\int \frac{ \cos x}{4+{ \sin }^{2}x}dx[/latex] over [latex]\left[-6,6\right][/latex]

Answer: Two graphs. The first shows the function f(x) = cos(x) / (4 + sin(x)^2). It is an oscillating function over [-6, 6] with turning points at roughly (-3, -2.5), (0, .25), and (3, -2.5), where (0,.25) is a local max and the others are local mins. The second shows the function F(x) = .5 * arctan(.5*sin(x)), which also oscillates over [-6,6]. It has turning points at roughly (-4.5, .25), (-1.5, -.25), (1.5, .25), and (4.5, -.25). The antiderivative is [latex]\frac{1}{2}\phantom{\rule{0.05em}{0ex}}{ \tan }^{-1}(\frac{ \sin x}{2})+C.[/latex] Taking [latex]C=\frac{1}{2}\phantom{\rule{0.05em}{0ex}}{ \tan }^{-1}(\frac{ \sin (6)}{2})[/latex] recovers the definite integral.

73. [T][latex]\int \frac{{e}^{x}}{1+{e}^{2x}}dx[/latex] over [latex]\left[-6,6\right][/latex]

In the following exercises, use a calculator to graph the antiderivative [latex]\int f[/latex] with [latex]C=0[/latex] over the given interval [latex]\left[a,b\right].[/latex] Approximate a value of C, if possible, such that adding C to the antiderivative gives the same value as the definite integral [latex]F(x)={\int }_{a}^{x}f(t)dt.[/latex]

74. [T][latex]\int \frac{1}{x\sqrt{{x}^{2}-4}}dx[/latex] over [latex]\left[2,6\right][/latex]

Answer: A graph of the function f(x) = -.5 * arctan(2 / ( sqrt(x^2 – 4) ) ) in quadrant four. It is an increasing concave down curve with a vertical asymptote at x=2. The antiderivative is [latex]\frac{1}{2}\phantom{\rule{0.05em}{0ex}}{ \sec }^{-1}(\frac{x}{2})+C.[/latex] Taking [latex]C=0[/latex] recovers the definite integral over [latex]\left[2,6\right].[/latex]

75. [T][latex]\int \frac{1}{(2x+2)\sqrt{x}}dx[/latex] over [latex]\left[0,6\right][/latex]

76. [T][latex]\int \frac{( \sin x+x \cos x)}{1+{x}^{2}{ \sin }^{2}x}dx[/latex] over [latex]\left[-6,6\right][/latex]

  The graph of f(x) = arctan(x sin(x)) over [-6,6]. It has five turning points at roughly (-5, -1.5), (-2,1), (0,0), (2,1), and (5,-1.5). The general antiderivative is [latex]{ \tan }^{-1}(x \sin x)+C.[/latex] Taking [latex]C=\text{−}{ \tan }^{-1}(6 \sin (6))[/latex] recovers the definite integral.

77. [T][latex]\int \frac{2{e}^{-2x}}{\sqrt{1-{e}^{-4x}}}dx[/latex] over [latex]\left[0,2\right][/latex]

78. [T][latex]\int \frac{1}{x+x{\text{ln}}^{2}x}[/latex] over [latex]\left[0,2\right][/latex]

A graph of the function f(x) = arctan(ln(x)) over (0, 2]. It is an increasing curve with x-intercept at (1,0). The general antiderivative is [latex]{ \tan }^{-1}(\text{ln}x)+C.[/latex] Taking [latex]C=\frac{\pi }{2}={ \tan }^{-1}\infty [/latex] recovers the definite integral.

79. [T][latex]\int \frac{{ \sin }^{-1}x}{\sqrt{1-{x}^{2}}}[/latex] over [latex]\left[-1,1\right][/latex]

In the following exercises, compute each definite integral.

80. [latex]{\int }_{0}^{1\text{/}2}\frac{ \tan ({ \sin }^{-1}t)}{\sqrt{1-{t}^{2}}}dt[/latex]

Answer: [latex]\frac{1}{2}\text{ln}(\frac{4}{3})[/latex]

81. [latex]{\int }_{1\text{/}4}^{1\text{/}2}\frac{ \tan ({ \cos }^{-1}t)}{\sqrt{1-{t}^{2}}}dt[/latex]

82. [latex]{\int }_{0}^{1\text{/}2}\frac{ \sin ({ \tan }^{-1}t)}{1+{t}^{2}}dt[/latex]

Answer:

[latex]1-\frac{2}{\sqrt{5}}[/latex]

83. [latex]{\int }_{0}^{1\text{/}2}\frac{ \cos ({ \tan }^{-1}t)}{1+{t}^{2}}dt[/latex]

84. For [latex]A>0,[/latex] compute [latex]I(A)={\int }_{\text{−}A}^{A}\frac{dt}{1+{t}^{2}}[/latex] and evaluate [latex]\underset{a\to \infty }{\text{lim}}I(A),[/latex] the area under the graph of [latex]\frac{1}{1+{t}^{2}}[/latex] on [latex]\left[\text{−}\infty ,\infty \right].[/latex]

Answer:

[latex]2{ \tan }^{-1}(A)\to \pi [/latex] as [latex]A\to \infty [/latex]

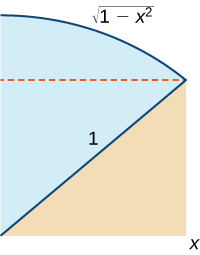
85. Use the following graph to prove that [latex]{\int }_{0}^{x}\sqrt{1-{t}^{2}}dt=\frac{1}{2}x\sqrt{1-{x}^{2}}+\frac{1}{2}\phantom{\rule{0.05em}{0ex}}{ \sin }^{-1}x.[/latex]

A diagram containing two shapes, a wedge from a circle shaded in blue on top of a triangle shaded in brown. The triangle’s hypotenuse is one of the radii edges of the wedge of the circle and is 1 unit long. There is a dotted red line forming a rectangle out of part of the wedge and the triangle, with the hypotenuse of the triangle as the diagonal of the rectangle. The curve of the circle is described by the equation sqrt(1-x^2).

Glossary

change of variables
the substitution of a variable, such as [latex]u[/latex], for an expression in the integrand
integration by substitution
a technique for integration that allows integration of functions that are the result of a chain-rule derivative

Licenses & Attributions

CC licensed content, Shared previously