We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

TEXT
Unlock Solution Steps
Sign in to
Symbolab
Get full access to all Solution Steps for any math problem
By continuing, you agree to our Terms of Use
and have read our Privacy Policy

Study Guides > College Algebra: Co-requisite Course

Domain and Range

Learning Objectives

  • Define the domain of functions from graphs
  • One-to-one functions
  • Use the horizontal line test to determine whether a function is one-to-one
Functions are a correspondence between two sets, called the domain and the range. When defining a function, you usually state what kind of numbers the domain (x) and range (f(x)) values can be. But even if you say they are real numbers, that doesn’t mean that all real numbers can be used for x. It also doesn’t mean that all real numbers can be function values, f(x). There may be restrictions on the domain and range. The restrictions partly depend on the type of function. In this topic, all functions will be restricted to real number values. That is, only real numbers can be used in the domain, and only real numbers can be in the range. There are two main reasons why domains are restricted.
  • You can’t divide by 0.
  • You can’t take the square (or other even) root of a negative number, as the result will not be a real number.

Find Domain and Range From a Graph

Finding domain and range of different functions is often a matter of asking yourself, what values can this function not have? Pictures make it easier to visualize what domain and range are, so we will show how to define the domain and range of functions given their graphs. What are the domain and range of the real-valued function [latex]f(x)=x+3[/latex]? This is a linear function. Remember that linear functions are lines that continue forever in each direction.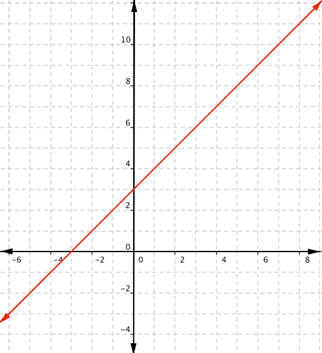 Line for f(x)=x+3 Any real number can be substituted for x and get a meaningful output. For any real number, you can always find an x value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range. The domain and range are all real numbers. For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.

Example

What are the domain and range of the real-valued function [latex]f(x)=−3x^{2}+6x+1[/latex]?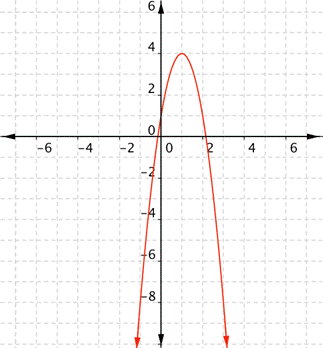 Downward-opening parabola with vertex of 1, 4.

Answer: This is a quadratic function. There are no rational (divide by zero) or radical (negative number under a root) expressions, so there is nothing that will restrict the domain. Any real number can be used for x to get a meaningful output. Because the coefficient of [latex]x^{2}[/latex] is negative, it will open downward. With quadratic functions, remember that there is either a maximum (greatest) value, or a minimum (least) value. In this case, there is a maximum value. The vertex, or high point, is at (1, 4). From the graph, you can see that [latex]f(x)\leq4[/latex].

Answer

The domain is all real numbers, and the range is all real numbers f(x) such that [latex]f(x)\leq4[/latex]. You can check that the vertex is indeed at (1, 4). Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value. The vertex must lie on the line of reflection, because it’s the only point that does not have a mirror image! In the previous example, notice that when [latex]x=2[/latex] and when [latex]x=0[/latex], the function value is 1. (You can verify this by evaluating f(2) and f(0).) That is, both (2, 1) and (0, 1) are on the graph. The line of reflection here is [latex]x=1[/latex], so the vertex must be at the point (1, f(1)). Evaluating f(1) gives [latex]f(1)=4[/latex], so the vertex is at (1, 4).

Example

What is the domain and range of the real-valued function [latex]f(x)=-2+\sqrt{x+5}[/latex]?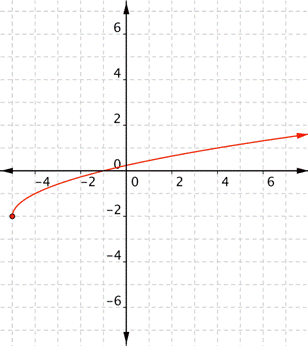 Radical function stemming from negative 5, negative 2.

Answer: This is a radical function. The domain of a radical function is any x value for which the radicand (the value under the radical sign) is not negative. That means [latex]x+5\geq0[/latex], so [latex]x\geq−5[/latex]. Since the square root must always be positive or 0, [latex] \displaystyle \sqrt{x+5}\ge 0[/latex]. That means [latex] \displaystyle -2+\sqrt{x+5}\ge -2[/latex].

Answer

The domain is all real numbers x where [latex]x\geq−5[/latex], and the range is all real numbers f(x) such that [latex]f(x)\geq−2[/latex].

Division by 0 could happen whenever the function has a variable in the denominator of a rational expression. That is, it’s something to look for in rational functions. Look at these examples, and note that “division by 0” doesn’t necessarily mean that x is 0! The following is an example of rational function, w will cover these in detail later.

Example

What is the domain of the real-valued function [latex] \displaystyle f(x)=\frac{3x}{x+2}[/latex]?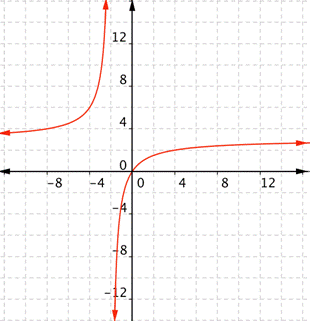 Rational function

Answer: This is a rational function. The domain of a rational function is restricted where the denominator is 0. In this case, [latex]x+2[/latex] is the denominator, and this is 0 only when [latex]x=−2[/latex].

Answer

The domain is all real numbers except [latex]−2[/latex]

In the following video we show how to define the domain and range of functions from their graphs. https://youtu.be/QAxZEelInJc

Example: Finding Domain and Range from a Graph

Find the domain and range of the function [latex]f[/latex]. Graph of a function from (-3, 1].

Answer: We can observe that the horizontal extent of the graph is –3 to 1, so the domain of [latex]f[/latex] is [latex]\left(-3,1\right][/latex]. Graph of the previous function shows the domain and range. The vertical extent of the graph is 0 to [latex]–4[/latex], so the range is [latex]\left[-4,0\right)[/latex].

Try It

[ohm_question]2316[/ohm_question]
 

Example: Finding Domain and Range from a Graph of Oil Production

Find the domain and range of the function [latex]f[/latex].
Graph of the Alaska Crude Oil Production where the y-axis is thousand barrels per day and the -axis is the years. (credit: modification of work by the U.S. Energy Information Administration)

Answer: The input quantity along the horizontal axis is "years," which we represent with the variable [latex]t[/latex] for time. The output quantity is "thousands of barrels of oil per day," which we represent with the variable [latex]b[/latex] for barrels. The graph may continue to the left and right beyond what is viewed, but based on the portion of the graph that is visible, we can determine the domain as [latex]1973\le t\le 2008[/latex] and the range as approximately [latex]180\le b\le 2010[/latex]. In interval notation, the domain is [1973, 2008], and the range is about [180, 2010]. For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.

Try It

Given the graph, identify the domain and range using interval notation. Graph of World Population Increase where the y-axis represents millions of people and the x-axis represents the year.

Answer: Domain = [1950, 2002]   Range = [47,000,000, 89,000,000]

Identify a One-to-One Function

Remember that in a function, the input value must have one and only one value for the output. There is a name for the set of input values and another name for the set of output values for a function. The set of input values is called the domain of the function. And the set of output values is called the range of the function. In the first example we remind you how to define domain and range using a table of values.

Example

Find the domain and range for the function.

x

y

−5

−6

−2

−1

−1

0

0

3

5

15

Answer: The domain is the set of inputs or x-coordinates.

[latex]\{−5,−2,−1,0,5\}[/latex]

The range is the set of outputs of y-coordinates.

[latex]\{−6,−1,0,3,15\}[/latex]

Answer

[latex-display]\begin{array}{l}\text{Domain}:\{−5,−2,−1,0,5\}\\\text{Range}:\{−6,−1,0,3,15\}\end{array}\\[/latex-display]

In the following video we show another example of finding domain and range from tabular data. https://youtu.be/GPBq18fCEv4 Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000. Figure of a bull and a graph of market prices.

However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.

Letter grade Grade point average
A 4.0
B 3.0
C 2.0
D 1.0

This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.

To visualize this concept, let’s look again at the two simple functions sketched in (a)and (b) of Figure 10.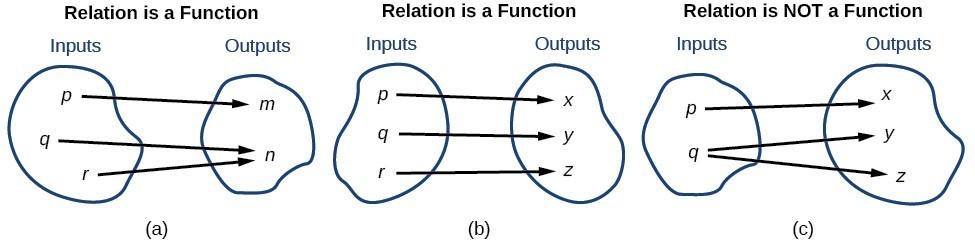
Three relations that demonstrate what constitute a function. Figure 10
The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.

A General Note: One-to-One Function

A one-to-one function is a function in which each output value corresponds to exactly one input value.

Example

Which table represents a one-to-one function? a)
input output
1 5
12 2
0 -1
4 2
-5 0
b)
input output
4 8
8 16
16 32
32 64
64 128

Answer: Table a) maps the output value 2 to two different input values, therefore this is NOT a one-to-one function. Table b) maps each output to one unique input, therefore this IS a one-to-one function.

Answer

Table b) is one-to-one

In the following video, we show an example of using tables of values to determine whether a function is one-to-one. https://youtu.be/QFOJmevha_Y

Using the Horizontal Line Test

An easy way to determine whether a function is a one-to-one function is to use the horizontal line test on the graph of the function.  To do this, draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.

How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.

  1. Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
  2. If there is any such line, determine that the function is not one-to-one.

Exercises

For the following graphs, determine which represent one-to-one functions. Graph of a polynomial.

Answer:

The function in (a) is not one-to-one. Using the horizontal line test, as shown below, it intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)

The function in (b) is one-to-one. Any horizontal line will intersect a diagonal line at most once. Graph of a line with three dashed horizontal lines passing through it. The function (c) is not one-to-one, and is in fact not a function. Graph of a circle with two dashed lines passing through horizontally

The following video provides another example of using the horizontal line test to determine whether a graph represents a one-to-one function. https://youtu.be/tbSGdcSN8RE

Summary

In real life and in algebra, different variables are often linked. When a change in value of one variable causes a change in the value of another variable, their interaction is called a relation. A relation has an input value which corresponds to an output value. When each input value has one and only one output value, that relation is a function. Functions can be written as ordered pairs, tables, or graphs. The set of input values is called the domain, and the set of output values is called the range.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download for Free at: http://cnx.org/contents/[email protected].
  • Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • Ex 1: Determine the Domain and Range of the Graph of a Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Determine if a Relation Given as a Table is a One-to-One Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Question ID#2316. Authored by: Lippman,David. License: CC BY: Attribution.