Read: Domain Restrictions
Learning Objectives
- Find the domain of a square root and rational function
- Find the domain and range of a function from the algebraic form.
- You can’t divide by [latex]0[/latex].
- You can’t take the square (or other even) root of a negative number, as the result will not be a real number.
- the function is a rational function and the denominator is [latex]0[/latex] for some value or values of x, [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex] is a rational function
- the function is a radical function with an even index (such as a square root), and the radicand can be negative for some value or values of x. [latex]f\left(x\right)=\sqrt{7-x}[/latex] is a radical function
| Function | Notes |
|---|---|
| [latex] f(x)=\dfrac{1}{x}[/latex] | If [latex]x=0[/latex], you would be dividing by [latex]0[/latex], so [latex]x\neq0[/latex]. |
| [latex] f(x)=\dfrac{2+x}{x-3}[/latex] | If [latex]x=3[/latex], you would be dividing by [latex]0[/latex], so [latex]x\neq3[/latex]. |
| [latex] f(x)=\dfrac{2(x-1)}{x-1}[/latex] | Although you can simplify this function to [latex]f(x)=2[/latex], when [latex]x=1[/latex] the original function would include division by [latex]0[/latex]. So [latex]x\neq1[/latex]. |
| [latex] f(x)=\dfrac{x+1}{{{x}^{2}}-1}[/latex] | Both [latex]x=1[/latex] and [latex]x=−1[/latex] would make the denominator 0. Again, this function can be simplified to [latex] f(x)=\dfrac{1}{x-1}[/latex], but when [latex]x=1[/latex] or [latex]x=−1[/latex] the original function would include division by 0, so [latex]x\neq1[/latex] and [latex]x\neq−1[/latex]. |
| [latex] f(x)=\dfrac{2(x-1)}{{{x}^{2}}+1}[/latex] | This is an example with no domain restrictions, even though there is a variable in the denominator. Since [latex]x^{2}\geq0,x^{2}+1[/latex] can never be [latex]0[/latex]. The least it can be is [latex]1[/latex], so there is no danger of division by [latex]0[/latex]. |
| Function | Restrictions to the Domain |
|---|---|
| [latex] f(x)=\sqrt{x}[/latex] | If [latex]x<0[/latex], you would be taking the square root of a negative number, so [latex]x\geq0[/latex]. |
| [latex] f(x)=\sqrt{x+10}[/latex] | If [latex]x<−10[/latex], you would be taking the square root of a negative number, so [latex]x\geq−10[/latex]. |
| [latex] f(x)=\sqrt{-x}[/latex] | When is [latex]-x[/latex] negative? Only when x is positive. (For example, if [latex]x=1[/latex], then [latex]−x=-1[/latex]. But if [latex]x=-3[/latex], then [latex]−x=3[/latex].) This means [latex]x\leq0[/latex]. |
| [latex] f(x)=\sqrt{{{x}^{2}}-1}[/latex] | [latex]x^{2}–1[/latex] must be positive, [latex]x^{2}–1>0[/latex]. So [latex]x^{2}>1[/latex]. This happens only when x is greater than 1 or less than [latex]−1[/latex]: [latex]x\leq−1[/latex] or [latex]x\geq1[/latex]. |
| [latex] f(x)=\sqrt{{{x}^{2}}+10}[/latex] | There are no domain restrictions, even though there is a variable under the radical. Since [latex]x^{2}\ge0[/latex], [latex]x^{2}+10[/latex] can never be negative. The least it can be is [latex]\sqrt{10}[/latex], so there is no danger of taking the square root of a negative number. |
How To: Given a function written in equation form, find the domain.
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Write the domain in interval form, if possible.
Example
Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].Answer: The input value, shown by the variable [latex]x[/latex] in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers. In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,\infty \right)[/latex].
How To: Given a function written in an equation form that includes a fraction, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . If the function’s formula contains an even root, set the radicand greater than or equal to [latex]0[/latex], and then solve.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example
Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].Answer: When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].
[latex]\begin{cases}2-x=0\hfill \\ -x=-2\hfill \\ x=2\hfill \end{cases}[/latex]
Now, we will exclude [latex]2[/latex] from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].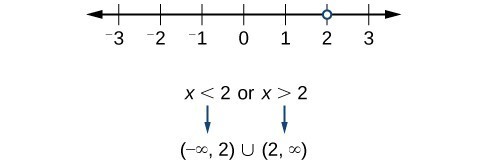 Figure 3
Figure 3How To: Given a function written in equation form including an even root, find the domain.
- Identify the input values.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
Example
Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].Answer: When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
[latex]\begin{cases}7-x\ge 0\hfill \\ -x\ge -7\hfill \\ x\le 7\hfill \end{cases}[/latex]
Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to [latex]7[/latex], or [latex]\left(-\infty ,7\right][/latex].Summary
Division by [latex]0[/latex] could happen whenever the function has a variable in the denominator of a rational expression. That is, it’s something to look for in rational functions. Look at these examples, and note that “division by [latex]0[/latex]” doesn’t necessarily mean that x is [latex]0[/latex]!Licenses & Attributions
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download for Free at: http://cnx.org/contents/[email protected].
