We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > MATH 0123

Radicals and Rational Exponents

Learning Outcomes

  • Evaluate and simplify square roots.
  • Rationalize a denominator that contains a square root.
  • Rewrite a radical expression using rational exponents.
A hardware store sells 16-ft ladders and 24-ft ladders. A window is located 12 feet above the ground. A ladder needs to be purchased that will reach the window from a point on the ground 5 feet from the building. To find out the length of ladder needed, we can draw a right triangle as shown in Figure 1, and use the Pythagorean Theorem.
A right triangle with a base of 5 feet, a height of 12 feet, and a hypotenuse labeled c Figure 1

[latex]\begin{align} {a}^{2}+{b}^{2}& = {c}^{2} \\ {5}^{2}+{12}^{2}& = {c}^{2} \\ 169& = {c}^{2} \end{align}[/latex]

Now we need to find out the length that, when squared, is 169, to determine which ladder to choose. In other word we need to find a square root. In this section we will investigate methods of finding solutions to problems such as this one.

Evaluate and Simplify Square Roots

When the square root of a number is squared, the result is the original number. Since [latex]{4}^{2}=16[/latex], the square root of [latex]16[/latex] is [latex]4[/latex]. The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root. In general terms, if [latex]a[/latex] is a positive real number, then the square root of [latex]a[/latex] is a number that, when multiplied by itself, gives [latex]a[/latex]. The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals [latex]a[/latex]. The square root obtained using a calculator is the principal square root. The principal square root of [latex]a[/latex] is written as [latex]\sqrt{a}[/latex]. The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.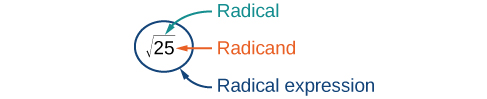 The expression: square root of twenty-five is enclosed in a circle. The circle has an arrow pointing to it labeled: Radical expression. The square root symbol has an arrow pointing to it labeled: Radical. The number twenty-five has an arrow pointing to it labeled: Radicand.

A General Note: Principal Square Root

The principal square root of [latex]a[/latex] is the nonnegative number that, when multiplied by itself, equals [latex]a[/latex]. It is written as a radical expression, with a symbol called a radical over the term called the radicand: [latex]\sqrt{a}[/latex].

Q & A

Does [latex]\sqrt{25}=\pm 5[/latex]?

No. Although both [latex]{5}^{2}[/latex] and [latex]{\left(-5\right)}^{2}[/latex] are [latex]25[/latex], the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is [latex]\sqrt{25}=5[/latex].

Example: Evaluating Square Roots

Evaluate each expression.
  1. [latex]\sqrt{100}[/latex]
  2. [latex]\sqrt{\sqrt{16}}[/latex]
  3. [latex]\sqrt{25+144}[/latex]
  4. [latex]\sqrt{49}-\sqrt{81}[/latex]

Answer:

  1. [latex]\sqrt{100}=10[/latex] because [latex]{10}^{2}=100[/latex]
  2. [latex]\sqrt{\sqrt{16}}=\sqrt{4}=2[/latex] because [latex]{4}^{2}=16[/latex] and [latex]{2}^{2}=4[/latex]
  3. [latex]\sqrt{25+144}=\sqrt{169}=13[/latex] because [latex]{13}^{2}=169[/latex]
  4. [latex]\sqrt{49}-\sqrt{81}=7 - 9=-2[/latex] because [latex]{7}^{2}=49[/latex] and [latex]{9}^{2}=81[/latex]

Q & A

For [latex]\sqrt{25+144}[/latex], can we find the square roots before adding?

No. [latex]\sqrt{25}+\sqrt{144}=5+12=17[/latex]. This is not equivalent to [latex]\sqrt{25+144}=13[/latex]. The order of operations requires us to add the terms in the radicand before finding the square root.

Try It

Evaluate each expression.
  1. [latex]\sqrt{225}[/latex]
  2. [latex]\sqrt{\sqrt{81}}[/latex]
  3. [latex]\sqrt{25 - 9}[/latex]
  4. [latex]\sqrt{36}+\sqrt{121}[/latex]

Answer:

  1. [latex]15[/latex]
  2. [latex]3[/latex]
  3. [latex]4[/latex]
  4. [latex]17[/latex]

Use the Product Rule to Simplify Square Roots

To simplify a square root, we rewrite it such that there are no perfect squares in the radicand. There are several properties of square roots that allow us to simplify complicated radical expressions. The first rule we will look at is the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite [latex]\sqrt{15}[/latex] as [latex]\sqrt{3}\cdot \sqrt{5}[/latex]. We can also use the product rule to express the product of multiple radical expressions as a single radical expression.

A General Note: The Product Rule for Simplifying Square Roots

If [latex]a[/latex] and [latex]b[/latex] are nonnegative, the square root of the product [latex]ab[/latex] is equal to the product of the square roots of [latex]a[/latex] and [latex]b[/latex].
[latex]\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex]

How To: Given a square root radical expression, use the product rule to simplify it.

  1. Factor any perfect squares from the radicand.
  2. Write the radical expression as a product of radical expressions.
  3. Simplify.

Example: Using the Product Rule to Simplify Square Roots

Simplify the radical expression.
  1. [latex]\sqrt{300}[/latex]
  2. [latex]\sqrt{162{a}^{5}{b}^{4}}[/latex]

Answer: 1. [latex-display]\begin{align}&\sqrt{100\cdot 3} && \text{Factor perfect square from radicand}. \\ &\sqrt{100}\cdot \sqrt{3} && \text{Write radical expression as product of radical expressions}. \\ &10\sqrt{3} && \text{Simplify}. \\ \text{ }\end{align}[/latex-display] 2. [latex-display]\begin{align}&\sqrt{81{a}^{4}{b}^{4}\cdot 2a} && \text{Factor perfect square from radicand}. \\ &\sqrt{81{a}^{4}{b}^{4}}\cdot \sqrt{2a} && \text{Write radical expression as product of radical expressions}. \\ &9{a}^{2}{b}^{2}\sqrt{2a} && \text{Simplify}. \end{align}[/latex-display]

Try It

Simplify [latex]\sqrt{50{x}^{2}{y}^{3}z}[/latex].

Answer: [latex]5|x||y|\sqrt{2yz}[/latex]. Notice the absolute value signs around x and y? That’s because their value must be positive!

How To: Given the product of multiple radical expressions, use the product rule to combine them into one radical expression.

  1. Express the product of multiple radical expressions as a single radical expression.
  2. Simplify.

Example: Using the Product Rule to Simplify the Product of Multiple Square Roots

Simplify the radical expression.

[latex]\sqrt{12}\cdot \sqrt{3}[/latex]

Answer:

[latex]\begin{align}&\sqrt{12\cdot 3} && \text{Express the product as a single radical expression}. \\ &\sqrt{36} && \text{Simplify}. \\ &6 \end{align}[/latex]

Try It

Simplify [latex]\sqrt{50x}\cdot \sqrt{2x}[/latex] assuming [latex]x>0[/latex].

Answer: [latex-display]10x[/latex-display] Because [latex]x>0[/latex], we do not need an absolute values.

Using the Quotient Rule to Simplify Square Roots

Just as we can rewrite the square root of a product as a product of square roots, so too can we rewrite the square root of a quotient as a quotient of square roots, using the quotient rule for simplifying square roots. It can be helpful to separate the numerator and denominator of a fraction under a radical so that we can take their square roots separately. We can rewrite [latex]\sqrt{\dfrac{5}{2}}[/latex] as [latex]\dfrac{\sqrt{5}}{\sqrt{2}}[/latex].

A General Note: The Quotient Rule for Simplifying Square Roots

The square root of the quotient [latex]\dfrac{a}{b}[/latex] is equal to the quotient of the square roots of [latex]a[/latex] and [latex]b[/latex], where [latex]b\ne 0[/latex].
[latex]\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}[/latex]

How To: Given a radical expression, use the quotient rule to simplify it.

  1. Write the radical expression as the quotient of two radical expressions.
  2. Simplify the numerator and denominator.

Example: Using the Quotient Rule to Simplify Square Roots

Simplify the radical expression.

[latex]\sqrt{\dfrac{5}{36}}[/latex]

Answer:

[latex]\begin{align}&\frac{\sqrt{5}}{\sqrt{36}} && \text{Write as quotient of two radical expressions}. \\ &\frac{\sqrt{5}}{6} && \text{Simplify denominator}. \end{align}[/latex]

Try It

Simplify [latex]\sqrt{\dfrac{2{x}^{2}}{9{y}^{4}}}[/latex].

Answer: [latex]\dfrac{x\sqrt{2}}{3{y}^{2}}[/latex]. We do not need the absolute value signs for [latex]{y}^{2}[/latex] because that term will always be nonnegative.

Example: Using the Quotient Rule to Simplify an Expression with Two Square Roots

Simplify the radical expression.

[latex]\dfrac{\sqrt{234{x}^{11}y}}{\sqrt{26{x}^{7}y}}[/latex]

Answer:

[latex]\begin{align}&\sqrt{\frac{234{x}^{11}y}{26{x}^{7}y}} && \text{Combine numerator and denominator into one radical expression}. \\ &\sqrt{9{x}^{4}} && \text{Simplify fraction}. \\ &3{x}^{2} && \text{Simplify square root}. \end{align}[/latex]

Try It

Simplify [latex]\dfrac{\sqrt{9{a}^{5}{b}^{14}}}{\sqrt{3{a}^{4}{b}^{5}}}[/latex].

Answer: [latex-display]{b}^{4}\sqrt{3ab}[/latex-display]

In the following video you will see more examples of how to simplify radical expressions with variables. https://youtu.be/q7LqsKPoAKo

Operations on Square Roots

We can add or subtract radical expressions only when they have the same radicand and when they have the same radical type such as square roots. For example, the sum of [latex]\sqrt{2}[/latex] and [latex]3\sqrt{2}[/latex] is [latex]4\sqrt{2}[/latex]. However, it is often possible to simplify radical expressions, and that may change the radicand. The radical expression [latex]\sqrt{18}[/latex] can be written with a [latex]2[/latex] in the radicand, as [latex]3\sqrt{2}[/latex], so [latex]\sqrt{2}+\sqrt{18}=\sqrt{2}+3\sqrt{2}=4\sqrt{2}[/latex].

How To: Given a radical expression requiring addition or subtraction of square roots, solve.

  1. Simplify each radical expression.
  2. Add or subtract expressions with equal radicands.

Example: Adding Square Roots

Add [latex]5\sqrt{12}+2\sqrt{3}[/latex].

Answer: We can rewrite [latex]5\sqrt{12}[/latex] as [latex]5\sqrt{4\cdot 3}[/latex]. According the product rule, this becomes [latex]5\sqrt{4}\sqrt{3}[/latex]. The square root of [latex]\sqrt{4}[/latex] is 2, so the expression becomes [latex]5\left(2\right)\sqrt{3}[/latex], which is [latex]10\sqrt{3}[/latex]. Now we can the terms have the same radicand so we can add.

[latex]10\sqrt{3}+2\sqrt{3}=12\sqrt{3}[/latex]

Try It

Add [latex]\sqrt{5}+6\sqrt{20}[/latex].

Answer: [latex-display]13\sqrt{5}[/latex-display]

Watch this video to see more examples of adding roots. https://youtu.be/S3fGUeALy7E

Example: Subtracting Square Roots

Subtract [latex]20\sqrt{72{a}^{3}{b}^{4}c}-14\sqrt{8{a}^{3}{b}^{4}c}[/latex].

Answer: Rewrite each term so they have equal radicands.

[latex]\begin{align} 20\sqrt{72{a}^{3}{b}^{4}c}& = 20\sqrt{9}\sqrt{4}\sqrt{2}\sqrt{a}\sqrt{{a}^{2}}\sqrt{{\left({b}^{2}\right)}^{2}}\sqrt{c} \\ & = 20\left(3\right)\left(2\right)a{b}^{2}\sqrt{2ac} \\ & = 120a{b}^{2}\sqrt{2ac}\\ \text{ } \end{align}[/latex]
[latex]\begin{align} 14\sqrt{8{a}^{3}{b}^{4}c}& = 14\sqrt{2}\sqrt{4}\sqrt{a}\sqrt{{a}^{2}}\sqrt{{\left({b}^{2}\right)}^{2}}\sqrt{c} \\ & = 14\left(2\right)a{b}^{2}\sqrt{2ac} \\ & = 28a{b}^{2}\sqrt{2ac} \end{align}[/latex]
Now the terms have the same radicand so we can subtract.
[latex]120a{b}^{2}\sqrt{2ac}-28a{b}^{2}\sqrt{2ac}=92a{b}^{2}\sqrt{2ac} \\ [/latex]
Note that we do not need an absolute value around the a because the [latex]a^3[/latex] under the radical means that a can't be negative.

Try It

Subtract [latex]3\sqrt{80x}-4\sqrt{45x}[/latex].

Answer: [latex-display]0[/latex-display]

in the next video we show more examples of how to subtract radicals. https://youtu.be/77TR9HsPZ6M

Rationalize Denominators

When an expression involving square root radicals is written in simplest form, it will not contain a radical in the denominator. We can remove radicals from the denominators of fractions using a process called rationalizing the denominator. We know that multiplying by 1 does not change the value of an expression. We use this property of multiplication to change expressions that contain radicals in the denominator. To remove radicals from the denominators of fractions, multiply by the form of 1 that will eliminate the radical. For a denominator containing a single term, multiply by the radical in the denominator over itself. In other words, if the denominator is [latex]b\sqrt{c}[/latex], multiply by [latex]\dfrac{\sqrt{c}}{\sqrt{c}}[/latex]. For a denominator containing the sum or difference of a rational and an irrational term, multiply the numerator and denominator by the conjugate of the denominator, which is found by changing the sign of the radical portion of the denominator. If the denominator is [latex]a+b\sqrt{c}[/latex], then the conjugate is [latex]a-b\sqrt{c}[/latex].

How To: Given an expression with a single square root radical term in the denominator, rationalize the denominator.

  1. Multiply the numerator and denominator by the radical in the denominator.
  2. Simplify.

Example: Rationalizing a Denominator Containing a Single Term

Write [latex]\dfrac{2\sqrt{3}}{3\sqrt{10}}[/latex] in simplest form.

Answer: The radical in the denominator is [latex]\sqrt{10}[/latex]. So multiply the fraction by [latex]\dfrac{\sqrt{10}}{\sqrt{10}}[/latex]. Then simplify.

[latex]\begin{align}\frac{2\sqrt{3}}{3\sqrt{10}}\cdot \frac{\sqrt{10}}{\sqrt{10}} &= \frac{2\sqrt{30}}{30} \\ &= \frac{\sqrt{30}}{15}\end{align}[/latex]

Try It

Write [latex]\dfrac{12\sqrt{3}}{\sqrt{2}}[/latex] in simplest form.

Answer: [latex-display]6\sqrt{6}[/latex-display]

How To: Given an expression with a radical term and a constant in the denominator, rationalize the denominator.

  1. Find the conjugate of the denominator.
  2. Multiply the numerator and denominator by the conjugate.
  3. Use the distributive property.
  4. Simplify.

Example: Rationalizing a Denominator Containing Two Terms

Write [latex]\dfrac{4}{1+\sqrt{5}}[/latex] in simplest form.

Answer: Begin by finding the conjugate of the denominator by writing the denominator and changing the sign. So the conjugate of [latex]1+\sqrt{5}[/latex] is [latex]1-\sqrt{5}[/latex]. Then multiply the fraction by [latex]\dfrac{1-\sqrt{5}}{1-\sqrt{5}}[/latex].

[latex]\begin{align}\frac{4}{1+\sqrt{5}}\cdot \frac{1-\sqrt{5}}{1-\sqrt{5}} &= \frac{4 - 4\sqrt{5}}{-4} && \text{Use the distributive property}. \\ &=\sqrt{5}-1 && \text{Simplify}. \end{align}[/latex]

Try It

Write [latex]\frac{7}{2+\sqrt{3}}[/latex] in simplest form.

Answer: [latex-display]14 - 7\sqrt{3}[/latex-display]

Nth Roots and Rational Exponents

Using Rational Roots

Although square roots are the most common rational roots, we can also find cube roots, 4th roots, 5th roots, and more. Just as the square root function is the inverse of the squaring function, these roots are the inverse of their respective power functions. These functions can be useful when we need to determine the number that, when raised to a certain power, gives a certain number. Suppose we know that [latex]{a}^{3}=8[/latex]. We want to find what number raised to the 3rd power is equal to 8. Since [latex]{2}^{3}=8[/latex], we say that 2 is the cube root of 8. The nth root of [latex]a[/latex] is a number that, when raised to the nth power, gives [latex]a[/latex]. For example, [latex]-3[/latex] is the 5th root of [latex]-243[/latex] because [latex]{\left(-3\right)}^{5}=-243[/latex]. If [latex]a[/latex] is a real number with at least one nth root, then the principal nth root of [latex]a[/latex] is the number with the same sign as [latex]a[/latex] that, when raised to the nth power, equals [latex]a[/latex]. The principal nth root of [latex]a[/latex] is written as [latex]\sqrt[n]{a}[/latex], where [latex]n[/latex] is a positive integer greater than or equal to 2. In the radical expression, [latex]n[/latex] is called the index of the radical.

A General Note: Principal nth Root

If [latex]a[/latex] is a real number with at least one nth root, then the principal nth root of [latex]a[/latex], written as [latex]\sqrt[n]{a}[/latex], is the number with the same sign as [latex]a[/latex] that, when raised to the nth power, equals [latex]a[/latex]. The index of the radical is [latex]n[/latex].

Example: Simplifying nth Roots

Simplify each of the following:
  1. [latex]\sqrt[5]{-32}[/latex]
  2. [latex]\sqrt[4]{4}\cdot \sqrt[4]{1,024}[/latex]
  3. [latex]-\sqrt[3]{\dfrac{8{x}^{6}}{125}}[/latex]
  4. [latex]8\sqrt[4]{3}-\sqrt[4]{48}[/latex]

Answer:

  1. [latex]\sqrt[5]{-32}=-2[/latex] because [latex]{\left(-2\right)}^{5}=-32 \\ \text{ }[/latex]
  2. First, express the product as a single radical expression. [latex]\sqrt[4]{4\text{,}096}=8[/latex] because [latex]{8}^{4}=4,096[/latex]
  3. [latex]\begin{align}\\ &\frac{-\sqrt[3]{8{x}^{6}}}{\sqrt[3]{125}} && \text{Write as quotient of two radical expressions}. \\ &\frac{-2{x}^{2}}{5} && \text{Simplify}. \\ \end{align}[/latex]
  4. [latex]\begin{align}\\ &8\sqrt[4]{3}-2\sqrt[4]{3} && \text{Simplify to get equal radicands}. \\ &6\sqrt[4]{3} && \text{Add}. \end{align}[/latex]

Try It

Simplify.
  1. [latex]\sqrt[3]{-216}[/latex]
  2. [latex]\dfrac{3\sqrt[4]{80}}{\sqrt[4]{5}}[/latex]
  3. [latex]6\sqrt[3]{9,000}+7\sqrt[3]{576}[/latex]

Answer:

  1. [latex]-6[/latex]
  2. [latex]6[/latex]
  3. [latex]88\sqrt[3]{9}[/latex]

Using Rational Exponents

Radical expressions can also be written without using the radical symbol. We can use rational (fractional) exponents. The index must be a positive integer. If the index [latex]n[/latex] is even, then [latex]a[/latex] cannot be negative.
[latex]{a}^{\frac{1}{n}}=\sqrt[n]{a}[/latex]
We can also have rational exponents with numerators other than 1. In these cases, the exponent must be a fraction in lowest terms. We raise the base to a power and take an nth root. The numerator tells us the power and the denominator tells us the root.
[latex]{a}^{\frac{m}{n}}={\left(\sqrt[n]{a}\right)}^{m}=\sqrt[n]{{a}^{m}}[/latex]
All of the properties of exponents that we learned for integer exponents also hold for rational exponents.

Rational Exponents

Rational exponents are another way to express principal nth roots. The general form for converting between a radical expression with a radical symbol and one with a rational exponent is
[latex]\begin{align}{a}^{\frac{m}{n}}={\left(\sqrt[n]{a}\right)}^{m}=\sqrt[n]{{a}^{m}}\end{align}[/latex]

How To: Given an expression with a rational exponent, write the expression as a radical.

  1. Determine the power by looking at the numerator of the exponent.
  2. Determine the root by looking at the denominator of the exponent.
  3. Using the base as the radicand, raise the radicand to the power and use the root as the index.

Example: Writing Rational Exponents as Radicals

Write [latex]{343}^{\frac{2}{3}}[/latex] as a radical. Simplify.

Answer: The 2 tells us the power and the 3 tells us the root.

[latex]{343}^{\frac{2}{3}}={\left(\sqrt[3]{343}\right)}^{2}=\sqrt[3]{{343}^{2}}[/latex]

We know that [latex]\sqrt[3]{343}=7[/latex] because [latex]{7}^{3}=343[/latex]. Because the cube root is easy to find, it is easiest to find the cube root before squaring for this problem. In general, it is easier to find the root first and then raise it to a power.

[latex]{343}^{\frac{2}{3}}={\left(\sqrt[3]{343}\right)}^{2}={7}^{2}=49[/latex]

Try It

Write [latex]{9}^{\frac{5}{2}}[/latex] as a radical. Simplify.

Answer: [latex-display]{\left(\sqrt{9}\right)}^{5}={3}^{5}=243[/latex-display]

Example: Writing Radicals as Rational Exponents

Write [latex]\dfrac{4}{\sqrt[7]{{a}^{2}}}[/latex] using a rational exponent.

Answer: The power is 2 and the root is 7, so the rational exponent will be [latex]\dfrac{2}{7}[/latex]. We get [latex]\dfrac{4}{{a}^{\frac{2}{7}}}[/latex]. Using properties of exponents, we get [latex]\dfrac{4}{\sqrt[7]{{a}^{2}}}=4{a}^{\frac{-2}{7}}[/latex].

Try It

Write [latex]x\sqrt{{\left(5y\right)}^{9}}[/latex] using a rational exponent.

Answer: [latex-display]x{\left(5y\right)}^{\frac{9}{2}}[/latex-display]

Watch this video to see more examples of how to write a radical with a fractional exponent. https://youtu.be/L5Z_3RrrVjA

Example: Simplifying Rational Exponents

Simplify:
  1. [latex]5\left(2{x}^{\frac{3}{4}}\right)\left(3{x}^{\frac{1}{5}}\right)[/latex]
  2. [latex]{\left(\dfrac{16}{9}\right)}^{-\frac{1}{2}}[/latex]

Answer: 1. [latex-display]\begin{align}&30{x}^{\frac{3}{4}}{x}^{\frac{1}{5}}&& \text{Multiply the coefficients}. \\ &30{x}^{\frac{3}{4}+\frac{1}{5}}&& \text{Use properties of exponents}. \\ &30{x}^{\frac{19}{20}}&& \text{Simplify}. \end{align}[/latex-display] 2. [latex-display]\begin{align}&{\left(\frac{9}{16}\right)}^{\frac{1}{2}}&& \text{Use definition of negative exponents}. \\ &\sqrt{\frac{9}{16}}&& \text{Rewrite as a radical}. \\ &\frac{\sqrt{9}}{\sqrt{16}}&& \text{Use the quotient rule}. \\ &\frac{3}{4}&& \text{Simplify}. \end{align}[/latex-display]

Try It

Simplify [latex]{\left(8x\right)}^{\frac{1}{3}}\left(14{x}^{\frac{6}{5}}\right)[/latex].

Answer: [latex-display]28{x}^{\frac{23}{15}}[/latex-display]

Key Concepts

  • The principal square root of a number [latex]a[/latex] is the nonnegative number that when multiplied by itself equals [latex]a[/latex].
  • If [latex]a[/latex] and [latex]b[/latex] are nonnegative, the square root of the product [latex]ab[/latex] is equal to the product of the square roots of [latex]a[/latex] and [latex]b[/latex]
  • If [latex]a[/latex] and [latex]b[/latex] are nonnegative, the square root of the quotient [latex]\frac{a}{b}[/latex] is equal to the quotient of the square roots of [latex]a[/latex] and [latex]b[/latex]
  • We can add and subtract radical expressions if they have the same radicand and the same index.
  • Radical expressions written in simplest form do not contain a radical in the denominator. To eliminate the square root radical from the denominator, multiply both the numerator and the denominator by the conjugate of the denominator.
  • The principal nth root of [latex]a[/latex] is the number with the same sign as [latex]a[/latex] that when raised to the nth power equals [latex]a[/latex]. These roots have the same properties as square roots.
  • Radicals can be rewritten as rational exponents and rational exponents can be rewritten as radicals.
  • The properties of exponents apply to rational exponents.

Glossary

index the number above the radical sign indicating the nth root principal nth root the number with the same sign as [latex]a[/latex] that when raised to the nth power equals [latex]a[/latex] principal square root the nonnegative square root of a number [latex]a[/latex] that, when multiplied by itself, equals [latex]a[/latex] radical the symbol used to indicate a root radical expression an expression containing a radical symbol radicand the number under the radical symbol

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Simplify Square Roots With Variables. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Question ID 14119. Authored by: James Sousa. License: CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
  • Question ID 109776, 110285, 110272, 110287, 110387. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Adding Radicals Requiring Simplification. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Subtracting Radicals. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Question ID 2049. Authored by: Lawrence Morales. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 110419. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 2765. Authored by: Bryan Johns. License: CC BY: Attribution.
  • Question ID 3441, 3415. Authored by: Jessica Reidel. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Ex: Write a Radical in Rational Exponent Form. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Question ID 2564, 2565, 2567, 2592. Authored by: Greg Langkamp. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 59783. Authored by: Gary Parker. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Specific attribution