Quadratic Equations
The computer monitor on the left in Figure 1 is a 23.6-inch model and the one on the right is a 27-inch model. Proportionally, the monitors appear very similar. If there is a limited amount of space and we desire the largest monitor possible, how do we decide which one to choose? In this section, we will learn how to solve problems such as this using four different methods. Figure 1
Figure 1Factoring and the Square Root Property
An equation containing a second-degree polynomial is called a quadratic equation. For example, equations such as [latex]2{x}^{2}+3x - 1=0[/latex] and [latex]{x}^{2}-4=0[/latex] are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics. Often the easiest method of solving a quadratic equation is factoring. Factoring means finding expressions that can be multiplied together to give the expression on one side of the equation. If a quadratic equation can be factored, it is written as a product of linear terms. Solving by factoring depends on the zero-product property, which states that if [latex]a\cdot b=0[/latex], then [latex]a=0[/latex] or [latex]b=0[/latex], where a and b are real numbers or algebraic expressions. In other words, if the product of two numbers or two expressions equals zero, then one of the numbers or one of the expressions must equal zero because zero multiplied by anything equals zero. Multiplying the factors expands the equation to a string of terms separated by plus or minus signs. So, in that sense, the operation of multiplication undoes the operation of factoring. For example, expand the factored expression [latex]\left(x - 2\right)\left(x+3\right)[/latex] by multiplying the two factors together.[latex]\begin{array}{l}\left(x - 2\right)\left(x+3\right)\hfill&={x}^{2}+3x - 2x - 6\hfill \\ \hfill&={x}^{2}+x - 6\hfill \end{array}[/latex]
The product is a quadratic expression. Set equal to zero, [latex]{x}^{2}+x - 6=0[/latex] is a quadratic equation. If we were to factor the equation, we would get back the factors we multiplied.
The process of factoring a quadratic equation depends on the leading coefficient, whether it is 1 or another integer. We will look at both situations; but first, we want to confirm that the equation is written in standard form, [latex]a{x}^{2}+bx+c=0[/latex], where a, b, and c are real numbers, and [latex]a\ne 0[/latex]. The equation [latex]{x}^{2}+x - 6=0[/latex] is in standard form.
We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF), and for equations that have special factoring formulas as well, such as the difference of squares, both of which we will see later in this section.
A General Note: The Zero-Product Property and Quadratic Equations
The zero-product property states[latex]\text{If }a\cdot b=0,\text{ then }a=0\text{ or }b=0[/latex],
where a and b are real numbers or algebraic expressions.
A quadratic equation is an equation containing a second-degree polynomial; for example
[latex]a{x}^{2}+bx+c=0[/latex]
where a, b, and c are real numbers, and if [latex]a\ne 0[/latex], it is in standard form.
Solving Quadratics with a Leading Coefficient of 1
In the quadratic equation [latex]{x}^{2}+x - 6=0[/latex], the leading coefficient, or the coefficient of [latex]{x}^{2}[/latex], is 1. We have one method of factoring quadratic equations in this form.How To: Given a quadratic equation with the leading coefficient of 1, factor it.
- Find two numbers whose product equals c and whose sum equals b.
- Use those numbers to write two factors of the form [latex]\left(x+k\right)\text{ or }\left(x-k\right)[/latex], where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and [latex]-2[/latex], the factors are [latex]\left(x+1\right)\left(x - 2\right)[/latex].
- Solve using the zero-product property by setting each factor equal to zero and solving for the variable.
Example: Factoring and Solving a Quadratic with Leading Coefficient of 1
Factor and solve the equation: [latex]{x}^{2}+x - 6=0[/latex].Answer: To factor [latex]{x}^{2}+x - 6=0[/latex], we look for two numbers whose product equals [latex]-6[/latex] and whose sum equals 1. Begin by looking at the possible factors of [latex]-6[/latex].
[latex]\begin{array}{l}1\cdot \left(-6\right)\hfill \\ \left(-6\right)\cdot 1\hfill \\ 2\cdot \left(-3\right)\hfill \\ 3\cdot \left(-2\right)\hfill \end{array}[/latex]
The last pair, [latex]3\cdot \left(-2\right)[/latex] sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.
[latex]\left(x - 2\right)\left(x+3\right)=0[/latex]
To solve this equation, we use the zero-product property. Set each factor equal to zero and solve.
[latex]\begin{array}{l}\left(x - 2\right)\left(x+3\right)\hfill&=0\hfill \\ \left(x - 2\right)\hfill&=0\hfill \\ x\hfill&=2\hfill \\ \left(x+3\right)\hfill&=0\hfill \\ x\hfill&=-3\hfill \end{array}[/latex]
The two solutions are [latex]x=2[/latex] and [latex]x=-3[/latex]. We can see how the solutions relate to the graph below. The solutions are the x-intercepts of [latex]{x}^{2}+x - 6=0[/latex].
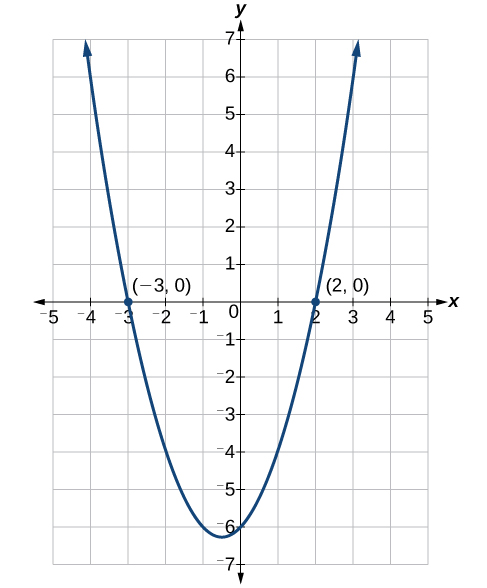
Try It
Factor and solve the quadratic equation: [latex]{x}^{2}-5x - 6=0[/latex].Answer: [latex]\left(x - 6\right)\left(x+1\right)=0;x=6,x=-1[/latex]
Using the Pythagorean Theorem
One of the most famous formulas in mathematics is the Pythagorean Theorem. It is based on a right triangle, and states the relationship among the lengths of the sides as [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], where [latex]a[/latex] and [latex]b[/latex] refer to the legs of a right triangle adjacent to the [latex]90^\circ [/latex] angle, and [latex]c[/latex] refers to the hypotenuse. It has immeasurable uses in architecture, engineering, the sciences, geometry, trigonometry, and algebra, and in everyday applications. We use the Pythagorean Theorem to solve for the length of one side of a triangle when we have the lengths of the other two. Because each of the terms is squared in the theorem, when we are solving for a side of a triangle, we have a quadratic equation. We can use the methods for solving quadratic equations that we learned in this section to solve for the missing side. The Pythagorean Theorem is given as[latex]{a}^{2}+{b}^{2}={c}^{2}[/latex]
where [latex]a[/latex] and [latex]b[/latex] refer to the legs of a right triangle adjacent to the [latex]{90}^{\circ }[/latex] angle, and [latex]c[/latex] refers to the hypotenuse.
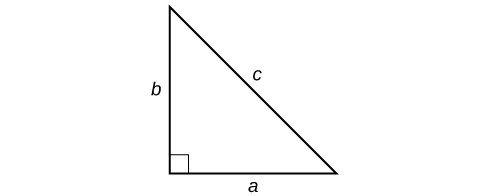 Figure 4
Figure 4Example: Finding the Length of the Missing Side of a Right Triangle
Find the length of the missing side of the right triangle.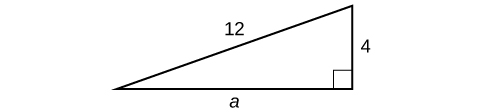
Answer: As we have measurements for side b and the hypotenuse, the missing side is a.
[latex]\begin{array}{l}{a}^{2}+{b}^{2}\hfill&={c}^{2}\hfill \\ {a}^{2}+{\left(4\right)}^{2}\hfill&={\left(12\right)}^{2}\hfill \\ {a}^{2}+16\hfill&=144\hfill \\ {a}^{2}\hfill&=128\hfill \\ a\hfill&=\sqrt{128}\hfill \\ \hfill&=8\sqrt{2}\hfill \end{array}[/latex]
Try It
Use the Pythagorean Theorem to solve the right triangle problem: Leg a measures 4 units, leg b measures 3 units. Find the length of the hypotenuse.Answer: [latex]5[/latex] units
The Discriminant
The quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions when we consider the discriminant, or the expression under the radical, [latex]{b}^{2}-4ac[/latex]. The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. The table below relates the value of the discriminant to the solutions of a quadratic equation.| Value of Discriminant | Results |
|---|---|
| [latex]{b}^{2}-4ac=0[/latex] | One rational solution (double solution) |
| [latex]{b}^{2}-4ac>0[/latex], perfect square | Two rational solutions |
| [latex]{b}^{2}-4ac>0[/latex], not a perfect square | Two irrational solutions |
| [latex]{b}^{2}-4ac<0[/latex] | Two complex solutions |
A General Note: The Discriminant
For [latex]a{x}^{2}+bx+c=0[/latex], where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers, the discriminant is the expression under the radical in the quadratic formula: [latex]{b}^{2}-4ac[/latex]. It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.Example: Using the Discriminant to Find the Nature of the Solutions to a Quadratic Equation
Use the discriminant to find the nature of the solutions to the following quadratic equations:- [latex]{x}^{2}+4x+4=0[/latex]
- [latex]8{x}^{2}+14x+3=0[/latex]
- [latex]3{x}^{2}-5x - 2=0[/latex]
- [latex]3{x}^{2}-10x+15=0[/latex]
Answer: Calculate the discriminant [latex]{b}^{2}-4ac[/latex] for each equation and state the expected type of solutions.
- [latex]{x}^{2}+4x+4=0[/latex][latex]{b}^{2}-4ac={\left(4\right)}^{2}-4\left(1\right)\left(4\right)=0[/latex]. There will be one rational double solution.
- [latex]8{x}^{2}+14x+3=0[/latex][latex]{b}^{2}-4ac={\left(14\right)}^{2}-4\left(8\right)\left(3\right)=100[/latex]. As [latex]100[/latex] is a perfect square, there will be two rational solutions.
- [latex]3{x}^{2}-5x - 2=0[/latex][latex]{b}^{2}-4ac={\left(-5\right)}^{2}-4\left(3\right)\left(-2\right)=49[/latex]. As [latex]49[/latex] is a perfect square, there will be two rational solutions.
- [latex]3{x}^{2}-10x+15=0[/latex][latex]{b}^{2}-4ac={\left(-10\right)}^{2}-4\left(3\right)\left(15\right)=-80[/latex]. There will be two complex solutions.
Key Concepts
- Many quadratic equations can be solved by factoring when the equation has a leading coefficient of 1 or if the equation is a difference of squares. The zero-factor property is then used to find solutions.
- Many quadratic equations with a leading coefficient other than 1 can be solved by factoring using the grouping method.
- Another method for solving quadratics is the square root property. The variable is squared. We isolate the squared term and take the square root of both sides of the equation. The solution will yield a positive and negative solution.
- Completing the square is a method of solving quadratic equations when the equation cannot be factored.
- A highly dependable method for solving quadratic equations is the quadratic formula, based on the coefficients and the constant term in the equation.
- The discriminant is used to indicate the nature of the roots that the quadratic equation will yield: real or complex, rational or irrational, and how many of each.
- The Pythagorean Theorem, among the most famous theorems in history, is used to solve right-triangle problems and has applications in numerous fields. Solving for the length of one side of a right triangle requires solving a quadratic equation.
Glossary
completing the square a process for solving quadratic equations in which terms are added to or subtracted from both sides of the equation in order to make one side a perfect square discriminant the expression under the radical in the quadratic formula that indicates the nature of the solutions, real or complex, rational or irrational, single or double roots. Pythagorean Theorem a theorem that states the relationship among the lengths of the sides of a right triangle, used to solve right triangle problems quadratic equation an equation containing a second-degree polynomial; can be solved using multiple methods quadratic formula a formula that will solve all quadratic equations square root property one of the methods used to solve a quadratic equation, in which the [latex]{x}^{2}[/latex] term is isolated so that the square root of both sides of the equation can be taken to solve for x zero-product property the property that formally states that multiplication by zero is zero, so that each factor of a quadratic equation can be set equal to zero to solve equationsLicenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 2029. Authored by: Lawrence Morales. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question 29172, 35145. Authored by: Jim Smart. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 48710. Authored by: Darlene Diaz. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 1384. Authored by: WebWork-Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 79619. Authored by: Edward Wicks. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
