Solutions for Sum and Difference Identities
Solutions to Try Its
1. [latex]\frac{\sqrt{2}+\sqrt{6}}{4}[/latex] 2. [latex]\frac{\sqrt{2}-\sqrt{6}}{4}[/latex] 3. [latex]\frac{1-\sqrt{3}}{1+\sqrt{3}}[/latex] 4. [latex]\cos \left(\frac{5\pi }{14}\right)[/latex] 5. [latex]\begin{array}{l}\tan \left(\pi -\theta \right)=\frac{\tan \left(\pi \right)-\tan \theta }{1+\tan \left(\pi \right)\tan \theta }\hfill \\ \text{ }=\frac{0-\tan \theta }{1+0\cdot \tan \theta }\hfill \\ \text{ }=-\tan \theta \hfill \end{array}[/latex]Solutions to Odd-Numbered Answers
1. The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if one of those angles measures [latex]x[/latex], the second angle measures [latex]\frac{\pi }{2}-x[/latex]. Then [latex]\sin x=\cos \left(\frac{\pi }{2}-x\right)[/latex]. The same holds for the other cofunction identities. The key is that the angles are complementary. 3. [latex]\sin \left(-x\right)=-\sin x[/latex], so [latex]\sin x[/latex] is odd. [latex]\cos \left(-x\right)=\cos \left(0-x\right)=\cos x[/latex], so [latex]\cos x[/latex] is even. 5. [latex]\frac{\sqrt{2}+\sqrt{6}}{4}[/latex] 7. [latex]\frac{\sqrt{6}-\sqrt{2}}{4}[/latex] 9. [latex]-2-\sqrt{3}[/latex] 11. [latex]-\frac{\sqrt{2}}{2}\sin x-\frac{\sqrt{2}}{2}\cos x[/latex] 13. [latex]-\frac{1}{2}\cos x-\frac{\sqrt{3}}{2}\sin x[/latex] 15. [latex]\csc \theta [/latex] 17. [latex]\cot x[/latex] 19. [latex]\tan \left(\frac{x}{10}\right)[/latex] 21. [latex]\sin \left(a-b\right)=\left(\frac{4}{5}\right)\left(\frac{1}{3}\right)-\left(\frac{3}{5}\right)\left(\frac{2\sqrt{2}}{3}\right)=\frac{4 - 6\sqrt{2}}{15}[/latex] [latex-display]\cos \left(a+b\right)=\left(\frac{3}{5}\right)\left(\frac{1}{3}\right)-\left(\frac{4}{5}\right)\left(\frac{2\sqrt{2}}{3}\right)=\frac{3 - 8\sqrt{2}}{15}[/latex-display] 23. [latex]\frac{\sqrt{2}-\sqrt{6}}{4}[/latex] 25. [latex]\sin x[/latex]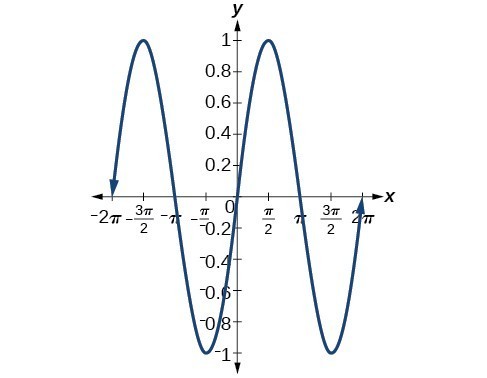 27. [latex]\cot \left(\frac{\pi }{6}-x\right)[/latex]
27. [latex]\cot \left(\frac{\pi }{6}-x\right)[/latex]
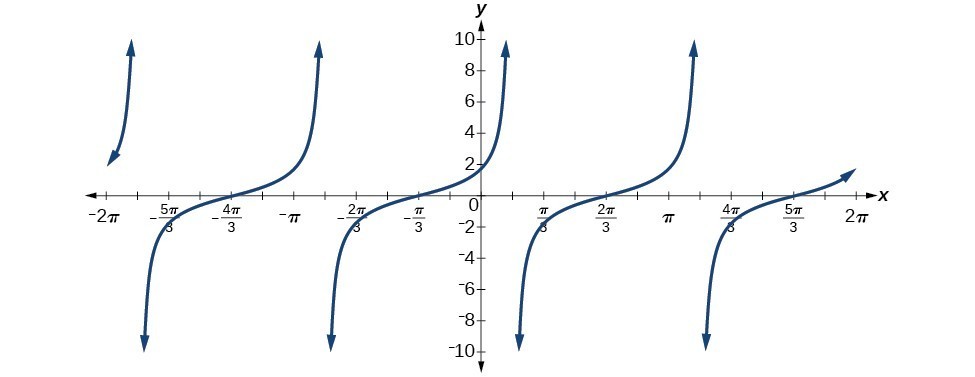 29. [latex]\cot \left(\frac{\pi }{4}+x\right)[/latex]
29. [latex]\cot \left(\frac{\pi }{4}+x\right)[/latex]
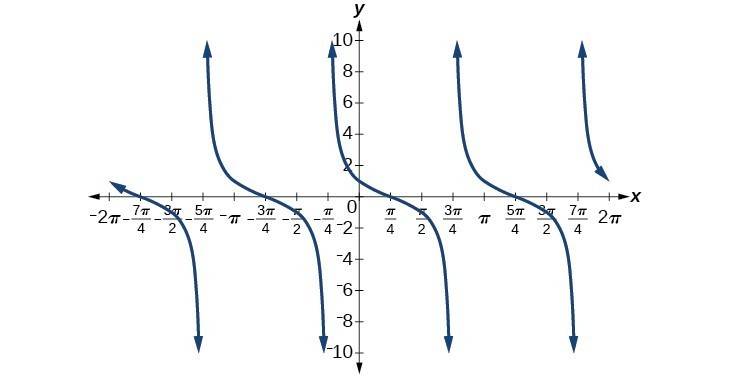 31. [latex]\frac{\sin x}{\sqrt{2}}+\frac{\cos x}{\sqrt{2}}[/latex]
31. [latex]\frac{\sin x}{\sqrt{2}}+\frac{\cos x}{\sqrt{2}}[/latex]
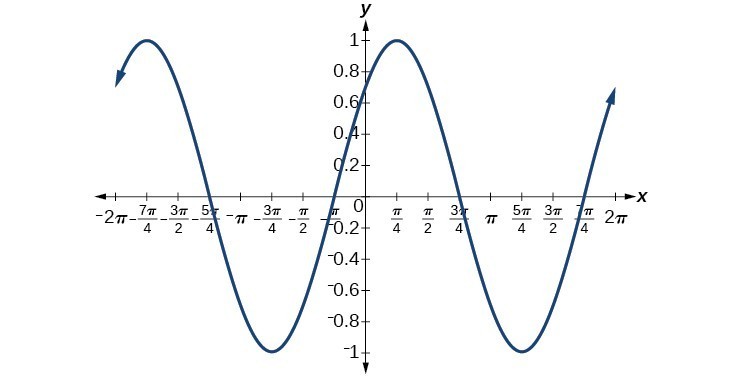 33. They are the same.
35. They are the different, try [latex]g\left(x\right)=\sin \left(9x\right)-\cos \left(3x\right)\sin \left(6x\right)[/latex].
37. They are the same.
39. They are the different, try [latex]g\left(\theta \right)=\frac{2\tan \theta }{1-{\tan }^{2}\theta }[/latex].
41. They are different, try [latex]g\left(x\right)=\frac{\tan x-\tan \left(2x\right)}{1+\tan x\tan \left(2x\right)}[/latex].
43. [latex]-\frac{\sqrt{3}-1}{2\sqrt{2}},\text{ or }-0.2588[/latex]
45. [latex]\frac{1+\sqrt{3}}{2\sqrt{2}}[/latex], or 0.9659
47. [latex]\begin{array}{c}\tan \left(x+\frac{\pi }{4}\right)=\\ \frac{\tan x+\tan \left(\frac{\pi }{4}\right)}{1-\tan x\tan \left(\frac{\pi }{4}\right)}=\\ \frac{\tan x+1}{1-\tan x\left(1\right)}=\frac{\tan x+1}{1-\tan x}\end{array}[/latex]
49. [latex]\begin{array}{c}\frac{\cos \left(a+b\right)}{\cos a\cos b}=\\ \frac{\cos a\cos b}{\cos a\cos b}-\frac{\sin a\sin b}{\cos a\cos b}=1-\tan a\tan b\end{array}[/latex]
51. [latex]\begin{array}{c}\frac{\cos \left(x+h\right)-\cos x}{h}=\\ \frac{\cos x\mathrm{cosh}-\sin x\mathrm{sinh}-\cos x}{h}=\\ \frac{\cos x\left(\mathrm{cosh}-1\right)-\sin x\mathrm{sinh}}{h}=\cos x\frac{\cos h - 1}{h}-\sin x\frac{\sin h}{h}\end{array}[/latex]
53. True
55. True. Note that [latex]\sin \left(\alpha +\beta \right)=\sin \left(\pi -\gamma \right)[/latex] and expand the right hand side.
33. They are the same.
35. They are the different, try [latex]g\left(x\right)=\sin \left(9x\right)-\cos \left(3x\right)\sin \left(6x\right)[/latex].
37. They are the same.
39. They are the different, try [latex]g\left(\theta \right)=\frac{2\tan \theta }{1-{\tan }^{2}\theta }[/latex].
41. They are different, try [latex]g\left(x\right)=\frac{\tan x-\tan \left(2x\right)}{1+\tan x\tan \left(2x\right)}[/latex].
43. [latex]-\frac{\sqrt{3}-1}{2\sqrt{2}},\text{ or }-0.2588[/latex]
45. [latex]\frac{1+\sqrt{3}}{2\sqrt{2}}[/latex], or 0.9659
47. [latex]\begin{array}{c}\tan \left(x+\frac{\pi }{4}\right)=\\ \frac{\tan x+\tan \left(\frac{\pi }{4}\right)}{1-\tan x\tan \left(\frac{\pi }{4}\right)}=\\ \frac{\tan x+1}{1-\tan x\left(1\right)}=\frac{\tan x+1}{1-\tan x}\end{array}[/latex]
49. [latex]\begin{array}{c}\frac{\cos \left(a+b\right)}{\cos a\cos b}=\\ \frac{\cos a\cos b}{\cos a\cos b}-\frac{\sin a\sin b}{\cos a\cos b}=1-\tan a\tan b\end{array}[/latex]
51. [latex]\begin{array}{c}\frac{\cos \left(x+h\right)-\cos x}{h}=\\ \frac{\cos x\mathrm{cosh}-\sin x\mathrm{sinh}-\cos x}{h}=\\ \frac{\cos x\left(\mathrm{cosh}-1\right)-\sin x\mathrm{sinh}}{h}=\cos x\frac{\cos h - 1}{h}-\sin x\frac{\sin h}{h}\end{array}[/latex]
53. True
55. True. Note that [latex]\sin \left(\alpha +\beta \right)=\sin \left(\pi -\gamma \right)[/latex] and expand the right hand side.Licenses & Attributions
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
