We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Boundless Algebra

Introduction to Quadratic Functions

What is a Quadratic Function?

Quadratic equations are second order polynomials, and have the form [latex]f(x)=ax^2+bx+c[/latex].

Learning Objectives

Describe the criteria for, and properties of, quadratic functions

Key Takeaways

Key Points

  • A quadratic function is of the form [latex]f(x)=ax^2+bx+c[/latex], where a is a nonzero constant, b and c are constants of any value, and x is the independent variable.
  • The solutions to a quadratic equation are known as its zeros, or roots.

Key Terms

  • dependent variable: Affected by a change in input, i.e. it changes depending on the value of the input.
  • independent variable: The input of a function that can be freely varied.
  • vertex: The minimum or maximum point of a quadratic function.
  • quadratic function: A function of degree two.
The single defining feature of quadratic functions is that they are of the second order, or of degree two. This means that in all quadratic functions, the highest exponent of [latex]x[/latex] in a non-zero term is equal to two.  A quadratic function is of the general form: [latex-display]f(x)=ax^2+bx+c[/latex-display] where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are constants and [latex]x[/latex] is the independent variable.  The constants [latex]b[/latex]and [latex]c[/latex] can take any finite value, and [latex]a[/latex] can take any finite value other than [latex]0[/latex]. A quadratic equation is a specific case of a quadratic function, with the function set equal to zero: [latex-display]ax^2+bx+c=0[/latex-display] When all constants are known, a quadratic equation can be solved as to find a solution of [latex]x[/latex].  Such solutions are known as zeros.  There are several ways of finding [latex]x[/latex], but these methods will be discussed later.

Differences Between Quadratics and Linear Functions

Quadratic equations are different than linear functions in a few key ways.
  • Linear functions either always decrease (if they have negative slope) or always increase (if they have positive slope). All quadratic functions both increase and decrease.
  • With a linear function, each input has an individual, unique output (assuming the output is not a constant).  With a quadratic function, pairs of unique independent variables will produce the same dependent variable, with only one exception (the vertex ) for a given quadratic function.
  • The slope of a quadratic function, unlike the slope of a linear function, is constantly changing.

Forms of Quadratic Functions

Quadratic functions can be expressed in many different forms. The form written above is called standard form. Additionally [latex-display]f(x)=a(x-x_1)(x-x_2)[/latex-display] is known as factored form, where [latex]x_1[/latex] and [latex]x_2[/latex] are the zeros, or roots, of the equation. These are [latex]x[/latex] values at which the function crosses the y-axis (and thus where [latex]y[/latex] equals zero). The vertex form is displayed as: [latex-display]f(x)=a(x-h)^2+k[/latex-display] where [latex]h[/latex] and [latex]k[/latex] are respectively the coordinates of the vertex, the point at which the function reaches either its maximum (if [latex]a[/latex] is negative) or minimum (if [latex]a[/latex] is positive).

The Quadratic Formula

The zeros of a quadratic equation can be found by solving the quadratic formula.

Learning Objectives

Solve for the roots of a quadratic function by using the quadratic formula

Key Takeaways

Key Points

  • The quadratic formula is: [latex]x=\frac{-b \pm \sqrt {b^2-4ac}}{2a}[/latex], where [latex]a[/latex] and [latex]b[/latex] are the coefficients of the [latex]x^2[/latex] and [latex]x[/latex] terms, respectively, in a quadratic equation, and [latex]c[/latex] is the value of the equation's constant.
  • To use the quadratic formula, [latex]ax^2 + bx+c [/latex] must equal zero and [latex]a[/latex] must not be zero.

Key Terms

  • zero: Also known as a root, an [latex]x[/latex] value at which the function of [latex]x[/latex] is equal to 0.
The quadratic formula is one tool that can be used to find the roots of a quadratic equation.  It is written: [latex-display]x=\dfrac{-b \pm \sqrt {b^2-4ac}}{2a}[/latex-display] where the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are the values of the coefficients in the quadratic equation: [latex-display]ax^2+bx+c=0[/latex-display] The quadratic formula can always be used to find the roots of a quadratic equation, regardless of whether the roots are real or complex, whole numbers or fractions, and so on.

Criteria For Use

To use the quadratic formula, two criteria must be satisfied:
  1. The quadratic equation must equal zero;  [latex]ax^2+bx+c=0[/latex]
  2. [latex]a[/latex] must not equal zero
The first criterion must be satisfied to use the quadratic formula because conceptually, the formula gives the values of [latex]x[/latex] where the quadratic function [latex]f(x) = ax^2+bx+c = 0[/latex]; the roots of the quadratic function. You can see why the second condition must be true by looking at the quadratic formula. If [latex]a=0[/latex], the denominator of the formula is zero, which results in an undefined quantity. Conceptually, this makes sense because if [latex]a=0[/latex], then the function [latex]f(x) = ax^2 + bx+c[/latex] is not quadratic, but linear!

Solving Quadratic Equations with the Quadratic Formula

Solutions to [latex-display]ax^2 + bx+c =0[/latex-display] can be found by using the quadratic formula [latex-display]x=\dfrac{-b \pm \sqrt {b^2-4ac}}{2a}[/latex-display] The symbol ± indicates there will be two solutions, one that involves adding the square root of [latex]b^2-4ac[/latex], and the other found by subtracting said square root. The resulting [latex]x[/latex] values (zeros) may or may not be distinct, and may or may not be real.

Example

Let's take a look at an example.  Suppose we want to find the roots of the following quadratic function: [latex-display]f(x) = 2x^2+5x+3[/latex-display] First, we need to set the function equal to zero, as the roots are where the function equals zero. [latex-display]0 = 2x^2+5x+3[/latex-display] Second, we need to identify the constants in the equation.  The value of [latex]a[/latex] is two, the value of [latex]b[/latex] is five, and the value of [latex]c[/latex] is three.  We can now substitute these values into the quadratic equation and simplify: [latex-display]x=\dfrac{-5 \pm \sqrt{5^2-4(2)(3)}}{2(2)}[/latex-display] [latex-display]x= \dfrac{-5 \pm \sqrt{25-24}}{4}[/latex-display] [latex-display]x = \dfrac{-5 \pm \sqrt{1}}{4}[/latex-display] [latex-display]\displaystyle x = \frac{-5}{4} + \frac{1}{4}[/latex], [latex]\displaystyle \frac{-5}{4} - \frac{1}{4}[/latex-display] [latex-display]x = \dfrac{-3}{4}[/latex], [latex]\dfrac{-6}{4}[/latex-display] [latex-display]x=\dfrac{-3}{4}[/latex], [latex]\dfrac{-3}{2}[/latex-display]

The Discriminant

The discriminant of a polynomial is a function of its coefficients that reveals information about the polynomial's roots.

Learning Objectives

Explain how and why the discriminant can be used to find the number of real roots of a quadratic equation

Key Takeaways

Key Points

  • [latex]\Delta =b^2-4ac[/latex] is the formula for a quadratic function 's discriminant.
  • If Δ is greater than zero, the polynomial has two real, distinct roots.
  • If Δ is equal to zero, the polynomial has only one real root.
  • If Δ is less than zero, the polynomial has no real roots, only two distinct complex roots.
  • A zero is the x value whereat the function crosses the x-axis. That is, it is the x-coordinate at which the function's value equals zero.

Key Terms

  • quadratic: Of degree two; can apply to polynomials.
  • zero: Also known as a root; an x value at which the function of x is equal to zero.
  • discriminant: An expression that gives information about the roots of a polynomial.
The discriminant of a quadratic function is a function of its coefficients that reveals information about its roots. A root is the value of the [latex]x[/latex] coordinate where the function crosses the [latex]x[/latex]-axis. That is, it is the [latex]x[/latex]-coordinate at which the function's value equals zero. The discriminant for quadratic functions is: [latex-display]\Delta = b^2-4ac[/latex-display] Where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are the coefficients in [latex]f(x) = ax^2 + bx + c[/latex]. The number of roots of the function can be determined by the value of [latex]\Delta[/latex].

The Discriminant and the Quadratic Formula

Recall the quadratic formula: [latex-display]{x=\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}}[/latex-display] where [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex]are the constants ([latex]a[/latex] must be non-zero) from a quadratic polynomial. The discriminant [latex]\Delta =b^2-4ac[/latex] is the portion of the quadratic formula under the square root.

Positive Discriminant

If [latex]{\Delta}[/latex] is positive, the square root in the quadratic formula is positive, and the solutions do not involve imaginary numbers. [latex-display]x={\dfrac{-b \pm \sqrt{\text{positive number}}}{2a}}[/latex-display] Because adding and subtracting a positive number will result in different values, a positive discriminant results in two distinct solutions, and two distinct roots of the quadratic function.

Zero Discriminant

If [latex]{\Delta}[/latex] is equal to zero, the square root in the quadratic formula is zero: [latex-display]x={\dfrac{-b \pm \sqrt{0}}{2a}}[/latex-display] Since adding zero and subtracting zero in the quadratic equation lead to the same outcome, there is only one distinct root of the quadratic function.

Negative Discriminant

If [latex]{\Delta}[/latex] is less than zero, the value under the square root in the quadratic formula is negative: [latex-display]x=\dfrac{-b \pm \sqrt{\text{negative number}}}{2a}[/latex-display] This means the square root itself is an imaginary number, so the roots of the quadratic function are distinct and not real.

Example

Consider the quadratic function: [latex-display]f(x)=x^2-x-2[/latex-display] Using [latex]1[/latex] as the value of [latex]a[/latex], [latex]-1[/latex] as the value of [latex]b[/latex], and [latex]-2[/latex] as the value of [latex]c[/latex], the discriminant of this function can be determined as follows: [latex-display]\Delta =(-1)^2-4\cdot 1 \cdot (-2)[/latex-display] [latex-display]\Delta =9[/latex-display] Because Δ is greater than zero, the function has two distinct, real roots. Checking graphically, we can confirm this is true; the zeros of the function can be found at [latex]x=-1[/latex] and [latex]x=2[/latex].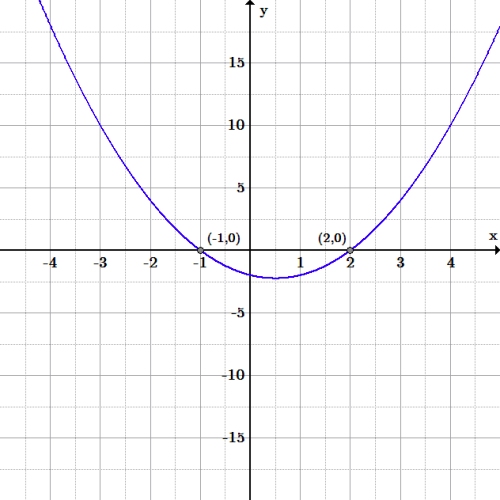
A parabola opening up with vertex at approximately (.5, -1). Example: Graph of a polynomial with the quadratic function [latex] f(x) = x^2 - x - 2[/latex]. Because the value is greater than 0, the function has two distinct, real zeros. The graph of shows that it clearly has two roots: the function crosses the [latex]x[/latex]-axis at [latex]x=-1[/latex] and [latex]x=2[/latex].

Other Equations in Quadratic Form

Many equations with no odd-degree terms can be reduced to quadratics and solved with the same methods as quadratics.

Learning Objectives

Use the quadratic formula to solve any equation in quadratic form

Key Takeaways

Key Points

  • A biquadratic equation (quartic equation with no terms of odd- degree ) has the form [latex]0=ax^4+bx^2+c[/latex]. It can be expressed as: [latex]0=ap^2+bp+c[/latex] (where [latex]p=x^2[/latex]).
  • The values of [latex]p[/latex] can be found by graphing, factoring, completing the square, or using the quadratic formula. Their square roots (positive and negative) are the values of [latex]x[/latex] that satisfy the original equation.
  • Higher-order equations can be solved by a similar process that involves reducing their exponents. The requirement is that there are two terms of [latex]x[/latex] such that the ratio of the highest exponent of [latex]x[/latex] to the lower is [latex]2:1[/latex].

Key Terms

  • zero: Also known as a root; an [latex]x[/latex] value at which the function of [latex]x[/latex] is equal to zero.
  • biquadratic: When a polynomial involves only the second and fourth powers of a variable.
  • quartic function: Any polynomial function whose greatest exponent is of power four.
Higher degree polynomial equations can be very difficult to solve. In some special situations, however, they can be made more manageable by reducing their exponents via substitution.  If a substitution can be made such that the higher order polynomial takes the form of a quadratic, any method for solving a quadratic equation can be applied. For example, if a quartic equation is biquadratic—that is, it includes no terms of an odd-degree— there is a quick way to find the zeroes of the quartic function by reducing it into a quadratic form. Consider a quadratic function with no odd-degree terms which has the form: [latex-display]0=ax^4+bx^2+c[/latex-display] If we let an arbitrary variable [latex]p[/latex] equal [latex]x^2[/latex], this can be reduced to an equation of a lower degree: [latex-display]0=ap^2+bp+c[/latex-display] With substitution, we were able to reduce a higher order polynomial into a quadratic equation.  It can now be solved with any of a number of methods (via graphing, factoring, completing the square, or by using the quadratic formula). Once values of [latex]p[/latex] are found, each positive value of the temporary variable [latex]p[/latex] can be used to find two values of [latex]x[/latex] such that: [latex-display]x=\sqrt p[/latex-display] As with every square root, the root of [latex]p[/latex] will have two values, one positive and one negative.  It is important to realize that the same kind of substitution can be done for any equation in quadratic form, not just quartics.

Example

As an example, consider the equation: [latex-display]0=x^4-12x^2+20[/latex-display]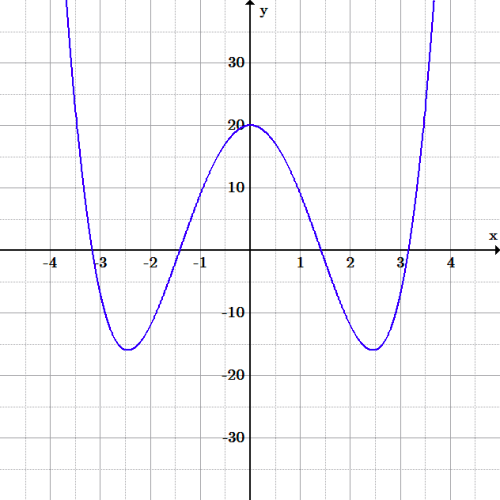
The function has symmetry over the y-axis and is shaped like a Quartic graph: Graph of the function [latex]f(x) = x^4-12x^2+20[/latex].

We can substitute the arbitrary variable [latex]p[/latex] in place of [latex]x^2[/latex]:

[latex-display]0=p^2-12p+20[/latex-display] This equation is now solvable for [latex]p[/latex] using the quadratic formula: [latex-display]p=\dfrac {12 \pm \sqrt {(-12)^2-4\cdot 1\cdot 20}}{2\cdot 1}[/latex-display] Simplifying this, we find [latex]p[/latex] equals 2 or 10. Knowing that [latex]p=x^2[/latex], we can use each value of [latex]p[/latex] to solve for two values of [latex]x[/latex]: [latex-display]x=\pm \sqrt 2[/latex] and [latex]x= \pm \sqrt 10[/latex-display] A similar procedure can be used to solve higher-order equations. The requirement is that there are two terms of [latex]x[/latex] such that the ratio of the highest exponent of [latex]x[/latex] to the lower is [latex]2:1[/latex].

Licenses & Attributions

CC licensed content, Shared previously

CC licensed content, Specific attribution