We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

TEXT
Unlock Solution Steps
Sign in to
Symbolab
Get full access to all Solution Steps for any math problem
By continuing, you agree to our Terms of Use
and have read our Privacy Policy

Study Guides > Mathematics for the Liberal Arts

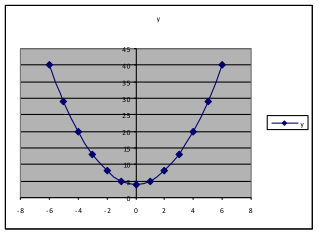
E1.10: Section 6 Part 2

Start exploring. How does changing h change the graph? Start by changing h to -2. That makes the spreadsheet look like the illustration below.
  A B C D E F G H
1 x y
2 -6 36 2 a
3 -5 22 -2 h
4 -4 12 4 k
5 -3 6
6 -2 4
7 -1 6
8 0 12
9 1 22
10 2 36
11 3 54
12 4 76
13 5 102
14 6 132
15
16
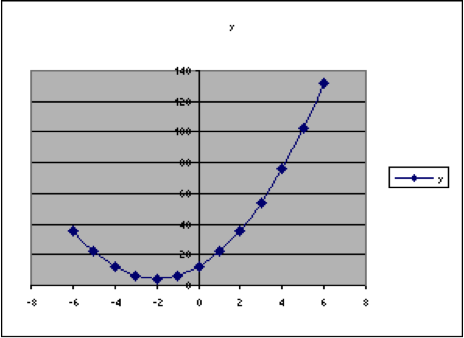Now we can notice that, when [latex]h=3[/latex], the lowest point on the graph is at [latex]x=3[/latex], and when [latex]h=-2[/latex], then the lowest point on the graph is at [latex]x=-2[/latex]. This suggests that maybe the value that is subtracted from x in the original formula is the one that determines where the lowest y-value is – that is, where the lowest point on the graph is.   Try [latex]h=0[/latex], [latex]h=4[/latex], and [latex]h=-3[/latex].  
[latex-display]h=0[/latex-display] (leaving [latex]a=2[/latex] and [latex]k=4[/latex]) [latex-display]h=4[/latex-display] (leaving [latex]a=2[/latex] and [latex]k=4[/latex]) [latex-display]h=-3[/latex-display] (leaving [latex]a=2[/latex] and [latex]k=4[/latex])
   
  Do these results support the conjecture we made in the previous sentence?   Answer: Yes.   Example 21.   Using the same formula and spreadsheet as in Example 18, use the values [latex]a=1[/latex], [latex]h=0[/latex], and explore the effect of changing k.
[latex-display]k=4[/latex-display] (leaving [latex]a=1[/latex] and [latex]h=0[/latex]) [latex-display]k=0[/latex-display] (leaving [latex]a=1[/latex] and [latex]h=0[/latex]) [latex-display]k=-7[/latex-display] (leaving [latex]a=1[/latex] and [latex]h=0[/latex])
   
We find that changing k alone changes how far up or down the lowest point on the graph is. It appears that the y-value of that lowest point is k. Example 22.   Using the same formula and spreadsheet as in Example 17, use [latex]h=0[/latex] and [latex]k=0[/latex], and explore the effect of changing a.
[latex-display]a=1[/latex-display] (with [latex]h=0[/latex] and [latex]k=0[/latex]) [latex-display]a=3[/latex-display] (with[latex]h=0[/latex] and [latex]k=0[/latex]) [latex-display]a=-3[/latex-display] (with [latex]h=0[/latex] and [latex]k=0[/latex])
   
We find that changing a from a positive to a negative number makes the graph change from opening upward to opening downward. Making a larger (from 1 to 3) changes how large the y-values are, so that the y-values for [latex]a=3[/latex] are three times as large as those when [latex]a=1[/latex].    

Licenses & Attributions

CC licensed content, Shared previously

  • Mathematics for Modeling. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution.